A Simplified E-graph Implementation
I’ve been spending some time mulling over e-graphs. I think I have it kind of pared down until it’s fairly simple. This implementation is probably not high performance as the main trick is removing a genuinely useful indexing structure. Still, this implementation is small enough that I can kind of keep it in my head. It has become rather cute.
For a user ready implementation of egraphs, see Metatheory https://github.com/0x0f0f0f/Metatheory.jl or egg https://egraphs-good.github.io/. For more motivation, see the egg paper or my first post https://www.philipzucker.com/egraph-1/
In a computer, terms like (a + b) * c are typically stored as trees. The EGraph converts this tree structure to one with an extra layer of indirection. Instead of nodes directly connecting to nodes, they connect first through a different kind of node labelled by an integer. These integer nodes are called eclasses and the modified original nodes are called enodes.
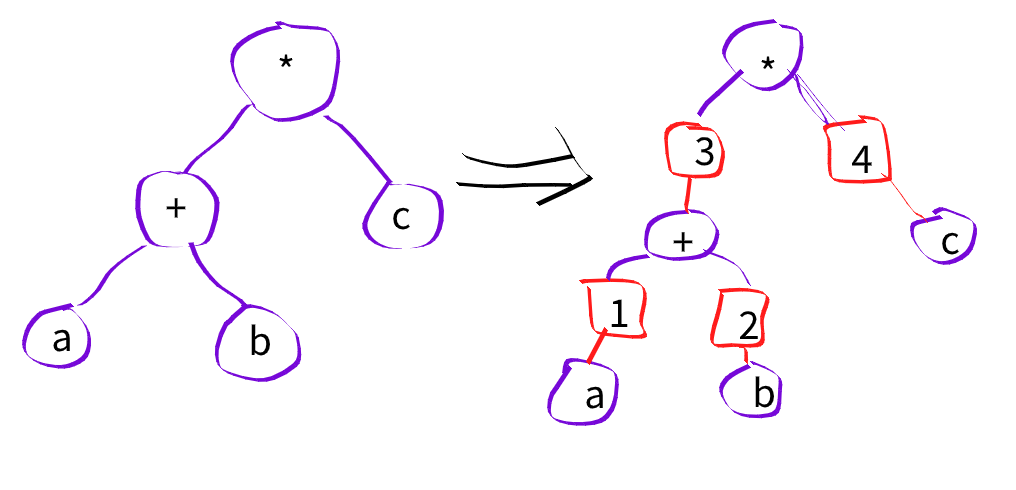
The EGraph is a bipartite directed graph between eclasses and enodes. ENodes belong uniquely to eclasses. Once we start merging eclasses, eclasses will point to more than one enode. The graph may also develop loops allowing representation in a sense of infinite terms.
Last time https://www.philipzucker.com/union-find-dict/, I built the abstraction of a union-find dict. This data structure allows you to retrieve information keyed on an equivalence class while still supporting the union operation. Given this piece, it is simple to define the two data structures.
@auto_hash_equals struct ENode
head::Symbol
args::Vector{Int64}
end
struct EGraph
eclass::IntDisjointMap
memo::Dict{ENode, Int64}
end
EGraph() = EGraph( IntDisjointMap(union) , Dict{ENode,Int64}())
The eclass field is a union-find dictionary from equivalence classes to vectors of ENodes. We tell the underlying IntDisjointMap that upon a union! of equivalence classes, we will union the enode vectors in the codomain of the IntDisjointMap to each other.
The memo table is not strictly necessary, but it gives us a good way to lookup which eclass an enode belongs to. Otherwise we’d have to brute force search the entire IntDisjointMap to find ENodes when we want them.
ENodes hold references to EClass ids, which unfortunately can go stale. We can canonize ENodes to use the freshest equivalence class indices.
canonize(G::EGraph, f::ENode) = ENode(f.head, [find_root(G.eclass, a) for a in f.args])
To add an ENode to the egraph first we canonize it, then we check if it already is in the memo table, and if not we actually push it in the IntDisjointMap and update the memo table.
function addenode!(G::EGraph, f::ENode)
f = canonize(G,f)
if haskey(G.memo, f)
return G.memo[f]
else
id = push!(G.eclass, [f])
G.memo[f] = id
return id
end
end
#convenience functions for pushing Julia Expr
addexpr!(G::EGraph, f::Symbol) = addenode!(G, ENode(f,[]))
function addexpr!(G::EGraph, f::Expr)
@assert f.head == :call
addenode!(G, ENode(f.args[1], [ addexpr!(G,a) for a in f.args[2:end] ] ))
end
When we assert an equality to an egraph, we take the union! of the two corresponding eclasses. We union! the underlying IntDisjointMap, then we recanonize all the held ENodes in that eclass and update the memo table.
function Base.union!(G::EGraph, f::Int64, g::Int64)
id = union!(G.eclass, f, g)
eclass = ENode[]
for enode in G.eclass[id]
delete!(G.memo, enode) # should we even bother with delete?
enode = canonize(G, enode) # should canonize return whether it did anything or not?
G.memo[enode] = id
push!(eclass, enode)
end
G.eclass[id] = eclass
end
That’s kind of it.
The big thing we haven’t discussed is calculating congruence closure. In my original presentation, this was a whole ordeal and the reason why we needed to maintain parent pointers from eclasses to enodes. This was very confusing.
Instead we can just find congruences via a brute force sweep over the egraph. This is inefficient compared to having likely candidates pointed out to us by the parent pointers. However, during naive ematching we are sweeping over the egraph anyway to find possible rewrite rules applications. This approach makes congruence closure feel rather similar to the other rewrite rules in the sense. There may be some utility in not considering congruence closure as a truly intrinsic part of the egraph. Perhaps you could use it for systems where congruence does not strictly hold?
An unfortunate thing is that congruences needs to be applied in worst case a number of time proportional to the depth of the egraph, as it only propagates congruences one layer at a time.
How it works: after a union! operation there are non canonical ENodes held in both memo and eclass. These noncanonical ENodes are exactly those who have arguments that include the eclass that was just turned into a child of another eclass. These are also exactly those ENodes that are candidates for congruence closure propagation. We can detect them during the sweep by canonization.
This expensive congruence sweep forgives more sins than the more efficient one. Something that can happen is that we try to addexpr! an ENode that is one of the stale ones, in other words it should be in the memo table but is not. This will falsely create a new eclass for this ENode. However, the congruence closure sweep will find this equivalence on the next pass.
# I forgot to include this IntDisjointMap iterator function in my last post.
# Conceptually it belongs there.
function Base.iterate(x::IntDisjointMap, state=1)
while state <= length(x.parents)
if x.parents[state] < 0
return ((state, x.values[state]) , state + 1)
end
state += 1
end
return nothing
end
# returns a list of tuples of found congruences
function congruences(G::EGraph)
buf = Tuple{Int64,Int64}[]
for (id1, eclass) in G.eclass #alternatively iterate over memo
for enode in eclass
cnode = canonize(G,enode)
if haskey(G.memo, cnode)
id2 = G.memo[cnode]
if id1 != id2
push!(buf, (id1,id2))
end
end
end
end
return buf
end
# propagate all congruences
function propagate_congruence(G::EGraph)
cong = congruences(G)
while length(cong) > 0
for (i,j) in cong
union!(G,i,j)
end
cong = congruences(G)
end
end
Bits and Bobbles
In principle I think this formulation makes it easier to parallelize congruence finding alongside rewrite rule matching. The rewriting process becomes a swapsies between finding tuples to union and actually applying them.
Everything in this post could probably be tuned up to be more efficient.
To add analyses, you want to store a compound structure in the IntDisjointMap. Tuple{Vector{ENode}, Analysis) The merge operation then does both enode merge and analysis merge.
Possibly changing enodes to be binary might be nice. One can compile arbitrary arity into this. Then everything fits in place in the appropriate arrays, removing significant indirection
Uses of egraphs:
My other implementation
- https://www.philipzucker.com/egraph-1/
- https://www.philipzucker.com/egraph-2/ egraph pattern matching
Edit: Max Willsey on twitter, an author of egg, says that egg originally took an approach to congruence like the above but found it too slow on larger workloads. It does indeed have a worse asymptotic performance than actually tracking parents and sniping the congruence locations. https://twitter.com/mwillsey/status/1378476707460509698?s=20
Some tests
using EGraphs
using Test
@testset "Basic EGraph" begin
G = EGraph()
a = addenode!(G, ENode(:a, []))
b = addenode!(G, ENode(:b, []))
#println(G)
union!(G, a, b)
#println(G)
@test addenode!(G, ENode(:a, [])) == 2
@test addenode!(G, ENode(:c, [])) == 3
@test addenode!(G, ENode(:f, [a])) == 4
union!(G, 3, 4)
#= println(G)
for (k,v) in G.eclass
println(k,v)
end =#
G = EGraph()
a = addenode!(G, ENode(:a, []))
b = addenode!(G, ENode(:b, []))
c = addenode!(G, ENode(:c, []))
union!(G, a, b)
fa = addenode!(G, ENode(:f, [a]))
fb = addenode!(G, ENode(:f, [b]))
fc = addenode!(G, ENode(:f, [c]))
ffa = addenode!(G, ENode(:f, [fa]))
ffb = addenode!(G, ENode(:f, [fb]))
@test congruences(G) == [(fa,fb)]
for (x,y) in congruences(G)
union!(G,x,y)
end
@test congruences(G) == [(ffa,ffb)]
union!(G, a, c)
@test congruences(G) == [(fc,fb), (ffa,ffb)]
for (x,y) in congruences(G)
union!(G,x,y)
end
@test congruences(G) == []
G = EGraph()
f5a = addexpr!(G, :( f(f(f(f(f(a))))) ))
f2a = addexpr!(G, :( f(f(a)) ))
@test length(G.eclass) == 6
union!(G , f5a, f2a)
@test find_root(G,f5a) == find_root(G,f2a)
@test length(G.eclass) == 5
f5a = addexpr!(G, :( f(f(f(f(f(a))))) ))
f2a = addexpr!(G, :( f(f(f(a))) ))
@test length(G.eclass) == 5
G = EGraph()
f5a = addexpr!(G, :( f(f(f(f(f(a))))) ))
fa = addexpr!(G, :( f(a) ))
a = addexpr!(G, :a)
@test length(G.eclass) == 6
union!(G , fa, a)
@test find_root(G,fa) == find_root(G,a)
propagate_congruence(G)
@test length(G.eclass) == 1
G = EGraph()
ffa = addexpr!(G, :( f(f(a)) ))
f5a = addexpr!(G, :( f(f(f(f(f(a))))) ))
a = addexpr!(G, :a)
@test length(G.eclass) == 6
union!(G , ffa, a)
@test find_root(G,ffa) == find_root(G,a)
propagate_congruence(G)
@test length(G.eclass) == 2
end