Categorical Combinators for Graphviz in Python
Graphviz is a graph visualization tool https://www.graphviz.org/. In Conal Elliott’s Compiling to categories http://conal.net/papers/compiling-to-categories/, compiling code to its corresponding graphviz representation was one very compelling example. These graphs are very similar to the corresponding string diagram of the monoidal category expression, but they also look like boolean circuit diagrams. Besides in Conal Elliott’s Haskell implementation, there is an implementation in the Julia Catlab.jl project https://epatters.github.io/Catlab.jl/stable/
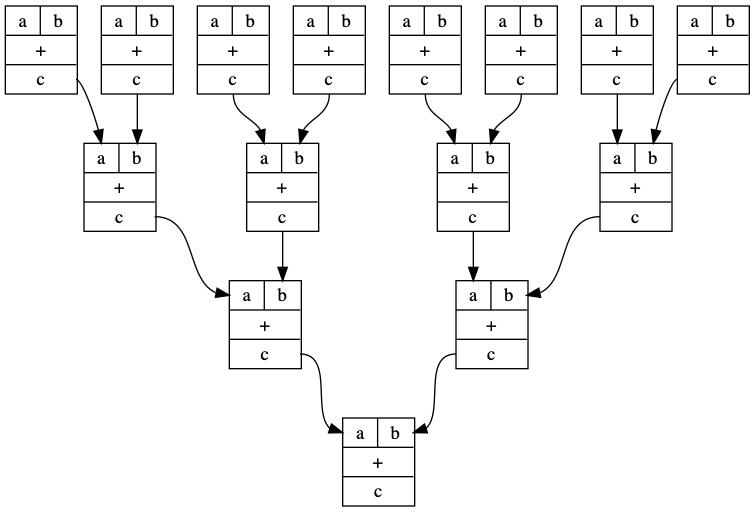
I’ve basically implemented a toy version of a similar thing in python. It lets you do things like this
plus = GraphCat.block("+", ["a","b"], ["c"])
I = GraphCat.idd()
p1 = plus
p2 = p1 @ (p1 * p1)
p3 = p1 @ (p2 * p2)
p4 = p1 @ (p3 * p3)
d = p4.run()
d.format = "png"
d.render("adders")
Why python?
- Python is the lingua franca of computing these days. Many people encounter it, even people whose main thing isn’t computers.
- The python ecosystem is nutso good.
- Julia is kind of an uphill battle for me. I’m fighting the battle ( https://github.com/philzook58/Rel.jl ) , but I already know python pretty well. I can rip this out and move on.
What I did was implement some wrappers around the graphviz python package. It exposes a not very feature rich stateful interface. It is pretty nice that it prints the graphs inline in jupyter notebooks though.
The code is written in a style very similar (and hopefully overloadable with) to that of z3py relation algebra. http://www.philipzucker.com/a-sketch-of-categorical-relation-algebra-combinators-in-z3py/ . There is a fairly general cookbook method here for categorifying dsl. Since graphviz does not directly expose fresh node creation as far as I can tell, I made my own using a random number generator. The actual combinators are graphviz object processors, so we build up a giant functional chain of processors and then actually execute it with run. The inputs and outputs are represented by lists of node names. The is some design space to consider here.
I also had to use class based wrappers Based on the precedent set by the python 3 matrix multiplication operator @, I think it is a requirement that this also be used for category composition. id is a keyword or something in python unfortunately. For monoidal product, I feel like overloading power ** looks nice even if it is a nonsensical analogy, * is also not too bad. I went with * for now.
The graphviz graphs aren’t quite string diagrams. They make no promise to preserve the ordering of your operations, but they seem to tend to.
import random
import graphviz
class GraphCat():
GC = GraphCat
def __init__(self,res): # just hold the graphviz processor function
self.res = res
def fresh(n): # makes random numbers for fresh node labels
return list([str(random.randint(0,1e9)) for i in range(n)])
def idd(): # identity morhism. 1 input 1 output.
def res(g):
#nodes = GC.fresh(n)
node = GC.fresh(1)[0]
#for node in nodes:
g.node(node, shape="point")
return [node], [node]
return GraphCat(res)
def compose(g, f): # compose morphisms. Makes graphviz edges between node labels generated by g and f
f = f.res
g = g.res
def res(G):
a, b = f(G)
b1, c = g(G)
assert(len(b) == len(b1))
G.edges(zip(b,b1))
return a, c
return GraphCat(res)
def par(f, g): #monoidal product. Puts f and g in parallel
f = f.res
g = g.res
def res(G):
a, b = f(G)
c, d = g(G)
return a + c, b + d
return GraphCat(res)
def dump(): # dump deletes this edge with an empty circle
def res(G):
node = GC.fresh(1)[0]
G.node(node, shape="point", fillcolor="white")
return [node], []
return GraphCat(res)
def dup(): # duplicate this edge
def res(G):
node = GC.fresh(1)[0]
G.node(node, shape="point", fillcolor="green")
return [node], [node, node]
return GraphCat(res)
def converse(f): # turn input to output of this combinator
f = f.res
def res(G):
a, b = f(G)
return b, a
return GraphCat(res)
def named_simple(name): # a simple labeled 1 input 1 output object
def res(G):
node = GC.fresh(1)[0]
G.node(node,name)
return [node], [node]
return GraphCat(res)
def block(name, inputs, outputs): # an object with labelled ports
inputs_label = [f"<{inp}> {inp}" for inp in inputs]
outputs_label = [f"<{outp}> {outp}" for outp in outputs]
#return # use graphviz to build block with label and n ports
def res(G):
node = GC.fresh(1)[0]
inputs1 = [f"{node}:{inp}" for inp in inputs]
outputs1 = [f"{node}:{outp}" for outp in outputs]
grphstring = "{ {" + " | ".join(inputs_label) + "} | " + name + " | {" + "|".join(outputs_label) + "} }"
G.node(node,grphstring, shape="record")
return inputs1, outputs1
return GC(res)
def fst(): # project out first par of tuple. semnatically equal to (id * dump)
return GraphCat.block("fst", ["a","b"], ["a1"])
def snd(): # dump * id
return GraphCat.block("fst", ["a","b"], ["b1"])
def run(self): # will run the object on a fresh graphviz object
dot = graphviz.Digraph()
self.res(dot)
return dot
def __matmul__(self, rhs): # matrix multiplication is a natural analog of composition
return GC.compose(self, rhs)
def __mul__(self, rhs): # monoidal product
return GC.par(self, rhs)
def __add__(self,rhs): # hmm. What should addition be? Join?
pass
def const(label): # inject a constant in. A labelled node with 1 outport and no input
def res(G):
node = GraphCat.fresh(1)[0]
G.node(node, str(label))
return [], [node]
return GC(res)
def cup():
def res(G):
nodes = GraphCat.fresh(2)
for node in nodes:
G.node(node, shape="point")
G.edge(nodes[0],nodes[1])
return [], nodes
return GraphCat(res)
def cap():
return GraphCat.converse(GraphCat.cup())
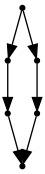
Here’s some example usage
cup = GraphCat.cup()
cap = GraphCat.cap()
d = cap @ (I * I) @ cup #(I * cap) @ (I * I * I) @ (cup * I)
d.run()
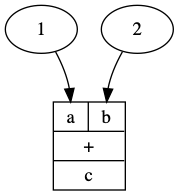
d = plus @ (GC.const(1) * GC.const(2))
d = d.run()
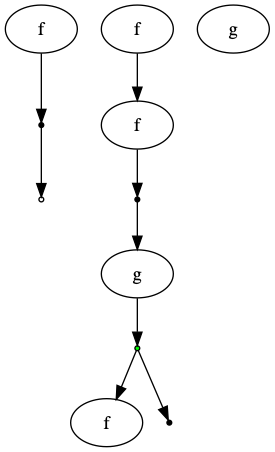
GC = GraphCat
f = GraphCat.named_simple("f")
g = GraphCat.named_simple("g")
I = GraphCat.idd()
dump = GC.dump()
dup = GC.dup()
diagram = ((f * I) @ dup @ g @ (dump * I) @ (I * f) @ (f * f)) * g
diagram.run()
Class based overloading is the main paradigm of overloading in python. You overload a program into different categories, by making a program take in the appropriate category class as a parameter.
# by passing in different category classes, we can make polymorphic functions
# They have to have a uniform interface though, which is hard to constrain in python.
def polymorphic_prog(M):
idd = M.idd()
dump = M.dump()
dup = M.dup()
return (idd * dump) @ dup
polymorphic_prog(GraphCat).run()
For example something like this ought to work. Then you can get the graph of some matrix computation to go along with it’s numpy implementation
class FinVect(np.ndarray):
def compose(f,g):
return f @ g
def idd(n):
return np.eye(n)
def par(f,g):
return np.kron(f,g)
def __mult__(self,rhs):
return np.kron(f,g)
# and so on.
Maybe outputting tikz is promising? https://github.com/negrinho/sane_tikz