Egglog 2: Automatically Proving the Pullback of a Monic is Monic

Egglog https://github.com/philzook58/egglog is a prolog-like syntax I’m fiddling with for the egg egraph library. Check out the online demo here http://www.philipzucker.com/egglog/ (rust compiles to wasm)

Last time I left off, I just had a syntax for the regular egg constructs of guarded rewrite rules basically. It turns out I wasn’t that far off from getting a prototype of prolog like rules working. And from that it was just a short hop and skip to doing something really cool. So here we go.

Categorical Diagram Chasing

A dragon I’ve been chasing for a while is how to do categorical reasoning automatically. Way back at the beginning I tried to prove that the pullback of a monic is monic https://www.philipzucker.com/category-theory-in-the-e-automated-theorem-prover/. I have reason to doubt that this exact encoding was sound, but I haven’t revisited it.

I had already been using egraphs to do equational reasoning in monoidal categories https://www.philipzucker.com/rust-category/ but I did not realize that they could also be very useful for reasoning about universal properties.

In principle diagram chasing should be easy. In a conversation with Cody Roux, he described his catnapp project https://github.com/codyroux/catnapp and how it was to go about solving these kinds of problems. According to him, diagram chasing involves discovering / building new objects, discovering / building new morphisms, recording equalities, and inspecting known morphisms and equalities to instantiate known universal properties. You can go about this in a bespoke way, but I think this procedure can be neatly encoded into the mechanisms egglog, since the horn clauses encode building new things and discovering new equalities, and egglog supports very strongly a notion of equality that seems useful here.

Well, now I have a bespoke theorem prover I’ve built for the very purpose!

And here’s my big theorem for the day: The pullback of a monic morphism is also monic.

To prove this we:

• Define composition and identity as constructions
• Make associavity and identity absorption as rewrite axioms
• Define all the morphisms and arrows to make a square
• define one arrow to be monic by giving the monic universal property
• define the square to be a pullback by saying it is commutative (an equality) and it’s universal condition
• Introduce the query by defining two new arbitrary morphisms and asking if they are equal.

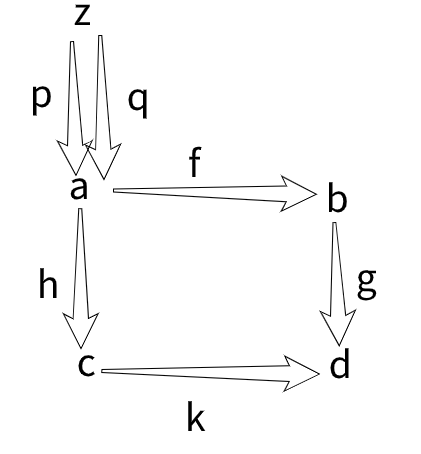
Here’s a little helper diagram to show what the morphisms and objects look like.

/* Axioms of category */

/* Typing rules */
/* identity exists */
type(id(A)) = hom(A,A) :- ob = type(A). 

/* Composition exists if types work out */
type(comp(F,G)) = hom(A,C) :- hom(A,B) = type(F), hom(B,C) = type(G).


/*
Identity abosrption
*/
F <- comp(id(A), F).
F <- comp(F, id(A)).


/* associativity of composition */
comp(comp(F,G),H) <-> comp(F, comp(G,H)).


/* specify types */
type(a) = ob.
type(b) = ob.
type(c) = ob.
type(d) = ob.

type(f) = hom(a,b).
type(g) = hom(b,d).
type(h) = hom(a,c).
type(k) = hom(c,d).

/* assume g is monic. I could possibly dispense with the type conditions as an optimization. */
F = H :- comp(F,g) = comp(H,g), hom(A,b) = type(F), hom(A,b) = type(H). 

/* square is pullback */
comp(f,g) = comp(h,k). /* square commutes */

/* universal triangle 1. There is a skolemization at play here */
comp(univ(F,H,E),h) = H
 :- comp(F,g) = comp(H,k), hom(E,b) = type(F), hom(E,c) = type(H).

/* universal triangle 2 */
comp(univ(F,H,E),f) = F
 :- comp(F,g) = comp(H,k), hom(E,b) = type(F), hom(E,c) = type(H).


/* uniqueness given square and triangles */
U = univ(F,H,E) :-
    comp(F,g) = comp(H,k), comp(U,h) = H, comp(U,f) = F, hom(E,b) = type(F), hom(E,c) = type(H).

/* Theorem:
h is monic. === forall P Q, comp(P,h) = comp(Q,h), dom(P) = dom(Q) => P = Q

We can take p and q to left of sequent, or intro them.
They are arbitrary symbols. We introduce the domain as z.
*/
type(z) = ob.
type(p) = hom(z,a).
type(q) = hom(z,a).
comp(p,h) = comp(q,h).

?- p = q

Note that this encoding heavily relies on the fact that only well typed terms get put into the egraph.

This does indeed return that p=q. I was beside myself when this worked. It is very fast too. Fractions of a second. I hope something hasn’t gone awry. You can try it yourself on the demo site for egglog http://www.philipzucker.com/egglog/ if you pick this example from the dropdown.

I also dumped the egraph into a visualization for this example. What is in there makes sense to my eye. It’s actually kind of interesting. Right click to open this in a new tab to really give it a look

Eggy bits

Egg rewrite rules are built around Searchers and Appliers, two traits that define functions to inspect and mutate the egraph. The right side of :- should correspond to a Searcher and the left side to an Applier. The interface defined by egg is slightly awkward for this purpose since it was designed with rewrite rules in mind. To get multipatterns working I defined the somewhat obvious struct.

struct MultiPattern<L> {
    patterns: Vec<EqWrap<Pattern<L>>>,
}

and implemented the Searcher trait for both EqWrap and MultiPattern. As a stop gap, the way I did this was by just using each held Pattern as a Searcher, and then merging the resulting variables bindings using the following function.

fn merge_subst2(s1: &Subst, s2: &Subst) -> Option<Subst> {
    let mut s1 = s1.clone();
    for (v, i) in s2.vec.iter() {
        match s1.insert(*v, *i) {
            // Oh actually we should check
            Some(i1) => {
                if *i != i1 {
                    return None;
                }
            }
            None => (),
        }
    }
    return Some(s1);
}

This is extremely wasteful, but doing better requires me to dig deeper into the egg library, as I don’t think the appropriate guts are exposed for me to do better. What I need is for a pattern when compiled to take in a set of already known variables and the search_eclass functions to take in an already known subst binding. This is a surmountable problem.

In addition to this, I added two new Appliers corresponding to an equality to the left of :- and a bare term. IgnoreApply is needed because the default Applier for Pattern will union with the incoming eclass id, which is not the semantics I want.

struct EqApply<L> {
    l: Pattern<L>,
    r: Pattern<L>,
}

struct IgnoreApply<L>(Pattern<L>);

After that it was just a matter of wiring it up to the frontend. It seems simple now, but this all took some digging.

Bits and Bobbles

• I’ve been thinking that there might some fun and useful partial evaluation to be had by using rust macros and the egg machine. Doesn’t help me though since in egglog everything is dynamically defined.
• Something akin to lambda prolog in the sense of supporting harrop formula seems doable and useful for expressivity. One can in principle match on the egraph to add new rules to the rule set, and a gensym facility would be very nice and these are natural semantics of forall quantifiers. I need some mechanism to abstract at least. Writing out the definition of pullback every time is not gonna fly. I’m not sure what is the answer here.
• Patterns in queries would be good and easy. I should just make queries Multipatterns and return the ematches array.
• I could add exists-unique as a basic construct too that skolemizes and expands. That would go a long ways.
• I have defined my queries in a doofy way.
• a repl would be cool. https://rust-cli.github.io/book/index.html I should improve the command line interface
• a s-exp input, command, and output format would be nice.