E-graphs are the data structure that efficiently compute with equalities between terms. It can be used to prove equivalences for equational reasoning, but also to find equational rewrites, which is useful for program transformations or algebraic simplification.

I got a hot tip from Talia Ringer on twitter about a paper and library called egg. Egg implements E-graphs as a performant generic library in Rust. The paper explains the data structure, a efficiency twist about when to fix its invariants, and shows some compelling use case studies. The claimed speedups over a naive implementation of E-graphs are absolutely nuts (x1000?!).

E-graphs compactly contain all the terms that are generated by a set of equalities and make it fast to perform the operation of congruence closure. Congruence is the property that $a = b \rightarrow f(a) = f(b)$ for all functions $f$. Functions take equals to equals. Congruence closure is taking an equivalence relation and closing it under this congruence operation, saturating the relation.

I decided to try parallel tracks of attempting to rebuild a version in Julia vs trying to build bindings to the implementation in egg. It is very unlikely I’ll beat the performance of egg, but native language flexibility is awful nice. Regardless I figured it’s a good learning experience.

SMT solvers like Z3 use E-graphs to reason about equality of uninterpreted functions. Understanding the E-graph structure has given me some possible insight into where I went wrong. Equality reasoning like this has been on my mind since I failed getting off-the-shelf provers to prove equations produced by Catlab.jl. So that’s sort of where I’m trying to head with this.

The actual E-graph data structure looks something like if a Union-Find and a Hash-Cons has a baby, so let’s talk about about those a bit.

Union Find or Disjoint Set Data Structure

The union find data structure is a fast data structure for representing partitions of sets.

Roughly how it works is that every element points to a parent in the partition. When you want to know what partition your thing is in, you follow the parent pointers up to a canonical element. While doing this you trickle the pointers upwards so the query will be faster next time. Eventually all the pointers in the partition will point directly to the canonical element with no indirection.

To merge two sets, set the parent pointer of one canonical element to the other.

That’s the rough sketch. There’s more in the wikipedia article https://en.wikipedia.org/wiki/Disjoint-set_data_structure. Julia has an implementation in the DataStructures.jl library https://juliacollections.github.io/DataStructures.jl/latest/disjoint_sets/ which I’m just going to use.

To start to see how union find is useful for equations, let’s say we have a pile of atoms :a :b :c :d and some equations :a = :c, :b = :d, :d = :c. Question: is :a = :b? For this small example you can see that it is, but the disjoint set structure will do the same.

using DataStructures
s = DisjointSets(:a,:b,:c,:d)
union!(s, :a, :c)
union!(s, :b, :d)
union!(s, :c, :d)
in_same_set(s,:a,:c)
# >>> true

Now the question is, how can we extend this to compound terms that appear in syntax trees like :(g(f(a)))? The trick is consider each subterm as an atom in it’s own right, :a, :(f(a)), :(g(f(a))) and place these things into the disjoint set. This trick is significantly aided by the technique of hash-consing, which brings the structure and performance differences between compound terms and atoms closer in alignment.

Hash-Consing

Hash-Consing is a programming technique to convert tree data structures into a DAG data structure where all identical subterms are shared rather than copied. This has the advantage of faster processing and decreased memory usage for trees with a lot of repetitive subterms and fast equality comparison since you can check the unique identity of a term immediately rather than recursing down it. The way this is done by identifying each node with a unique id and maintaining a mapping of nodes to ids in a hash table. Whenever you create new nodes, you use smart constructors that first check if the node is already defined in the hash table. If it is, this canonical node is returned, otherwise the node is added to the hash table.

You can recursively convert a tree into it’s hash consed from by destructing it and reconstructing it with the smart constructors. The unique id may be the memory address where the node is stored or it may come from a counter being incremented every time you create a novel term.

The canonical reference on hash-consing is Type-Safe Modular Hash-Consing. Hash consing has been folklore for a very, very long time though. There is a reference in here to a paper by Ershov in 1958 for example. A really fun example in there is using HashConsing for a BDD implementation.

Another term sometimes used is “interned”. Julia’s Symbol is interned.

E-Graphs

When we’re talking about equations, it no longer makes sense to give each term an id as in the pure hash-cons. Instead we want to give each equivalence class of terms a unique id and maintain the equivalence classes in a union-find structure. As we put more equalities into the union-find structure and the equivalence classes grow, these canonical ids change under our feet, which is annoying but manageable.

The E-graph maintains:

  • a map from hash-consed terms to class ids
  • a map from class-ids to equivalence classes
  • a unionfind data structure on class ids

Each equivalence class needs to maintain

  • an array of terms in the class
  • an array of possible parent terms for efficiently propagating congruences

We will index into congruence classes with Id. Wrapping the Int64 in a struct should have no performance cost, and keeps things sane.

struct Id
    id::Int64
end

We need a structure to hold hash consed terms of our language. AutoHashEquals.jl makes it so hash and == use a structural definition.

using AutoHashEquals
@auto_hash_equals mutable struct Term
    head::Symbol
    args::Array{Id}
end

An equivalence class is a set of nodes. We also need to store parents of these nodes in order to make congruence closure and hash cons updating fast.

mutable struct EClass
    nodes::Array{Term}
    parents::Array{Tuple{Term,Id}}
end

Finally we have the actual EGraph data structure. It holds a unionfind that keeps equivalences of classes, a memo field to map Term to their equivalence class, a classes field to map equivalence class Id to the EClass. Maintaining all the appropriate invariants and connections between these pieces sucks.

using DataStructures

mutable struct EGraph
    unionfind::IntDisjointSets
    memo::Dict{Term,Id} # int32 UInt32?
    classes::Dict{Id,EClass} # Use array?
    dirty_unions::Array{Id}
end

# Build an empty EGraph
EGraph() = EGraph(IntDisjointSets(0), Dict(), Dict(), [])

Finding the root class or querying whether in_same_set for an Id just passes off the query to the union find.

# returns the canonical Id
find_root!(e::EGraph, id::Id) = Id(DataStructures.find_root!(e.unionfind, id.id))

in_same_class(e::EGraph, t1::Term, t2::Term) = in_same_set(e.unionfind, e.memo[t1] , e.memo[t2])

We can canonicalize terms so that the Id arguments only point to the root class.

function canonicalize!(e::EGraph, t::Term)
    t.args = [ find_root!(e, a) for a in t.args ]
end

We can lookup the class a term belongs to by canonicalizing and using the memo table

function find_class!(e::EGraph, t::Term)  # lookup
    canonicalize!(e, t) #t.args = [ find_root!(e, a) for a in t.args ]  # canonicalize the term
    if haskey(e.memo, t)
        id = e.memo[t]
        return find_root!(e, id)
    else
        return nothing
    end
end

We can add new terms by finding if they already exist in the hashcons. If so it, it does nothing. But if not, we need to make a new EClass for this term to live in. This is the only way new EClasses are made. It is important to maintain the hashcons correctly and canonicalize so that we don’t accidentally create a new EClass for a term that should already be in another EClass.

function Base.push!(e::EGraph, t::Term)
    id = find_class!(e,t) # also canonicalizes t
    if id == nothing # term not in egraph. Make new class and put in graph
        id = Id(push!(e.unionfind))
        cls = EClass( [t] , [] )
        for child in t.args # set parent pointers
            push!(e.classes[child].parents,  (t, id))
        end
        e.classes[id] = cls
        e.memo[t] = id
        return id
    else
        return id
    end
end

Alright. Here is where stuff gets hairy. We want to union two equivalence classes.

  1. Cananonize the Id.
  2. Check if already equivalent. If so, we’re done
  3. Ask unionfind to perform union
  4. Recanonize the arguments of nodes in memo
  5. Merge nodes and parents arrays of the two eclasses
  6. Mark equivalence class as dirty for rebuilding.
  7. Destroy the unneeded EClass in classes
function Base.union!(e::EGraph, id1::Id, id2::Id)
    id1 = find_root!(e, id1)
    id2 = find_root!(e, id2)
    # An invariant is that the EClass data should always keyed with the root of the union find
    # in the e.classes datastructure
    if id1 != id2 # if not already in same class
        id3 = Id(union!(e.unionfind, id1.id,id2.id)) # perform the union find
        if id3 == id1 # picked id1 as root
            to = id1
            from = id2
        elseif id3 == id2 # picked id2 as root
            to = id2
            from = id1
        else
            @assert false
        end
            
        push!(e.dirty_unions, id3) # id3 will need it's parents processed in rebuild!
        
        # we empty out the e.class[from] and put everything in e.class[to]
        for t in e.classes[from].nodes
            push!(e.classes[to].nodes, t) 
        end
        
        # recanonize all nodes in memo.
        for t in e.classes[to].nodes
            delete!(e.memo, t) # remove stale term
            canonicalize!(e, t) # update term in place in nodes array
            e.memo[t] = to # now this term is in the to eqauivalence class
        end
        
        # merge parents list
        for (p,id) in e.classes[from].parents
            push!(e.classes[to].parents, (p, find_root!(e,id)))
        end
        
        # destroy "from" from e.classes. It's information should now be
        # in e.classes[to] and it should never be accessed.
        delete!(e.classes, from) 
    end 
        
end

This code might be right. Lemme tell ya, I’ve had versions only subtly different that weren’t right. So I dunno. Buyer beware.

Finally the last big chunk is rebuild!. This function works through the dirty_unions array and fixes parent nodes and propagates any congruences.


function repair!(e::EGraph, id::Id)
    cls = e.classes[id]
    
    #  for every parent, update the hash cons. We need to repair that the term has possibly a wrong id in it
    for (t,t_id) in cls.parents
        delete!( e.memo, t) # the parent should be updated to use the updated class id
        canonicalize!(e, t) # canonicalize
        e.memo[t] = find_root!(e, t_id) # replace in hash cons  
    end
    
    # now we need to discover possible new congruence eqaulities in the parent nodes.
    # we do this by building up a parent hash to see if any new terms are generated.
    new_parents = Dict()
    for (t,t_id) in cls.parents
        canonicalize!(e,t) # canonicalize. Unnecessary by the above?
        if haskey(new_parents, t)
            union!(e, t_id, new_parents[t])
        end
        new_parents[t] = find_root!(e, t_id)
    end
    e.classes[id].parents = [ (p,id) for (p,id) in new_parents]
end

function rebuild!(e::EGraph)
    while length(e.dirty_unions) > 0
       todo = Set([ find_root!(e,id) for id in e.dirty_unions])
       e.dirty_unions = []
       for id in todo
            repair!(e, id)
        end
    end
end

Here’s some helper functions to build constants and terms

function constant!(e::EGraph, x::Symbol)
      t = Term(x, [])
      push!(e, t)
end

term!(e::EGraph, f::Symbol) = (args...) -> begin
    t = Term(f, collect(args))
    push!(e,  t)
end

and some other helper functions to help draw the EGraph, which is pretty crucial

using LightGraphs
using GraphPlot
using Colors

function graph(e::EGraph) 
    nverts = length(e.memo)
    g = SimpleDiGraph(nverts)
    vertmap = Dict([ t => n for (n, (t, id)) in enumerate(e.memo)])
    #=for (id, cls) in e.classes
        for t1 in cls.nodes
            for (t2,_) in cls.parents
                add_edge!(g, vertmap[t2], vertmap[t1])
            end
        end
    end =#
    for (n,(t,id)) in enumerate(e.memo)
        for n2 in t.args
            for t2 in e.classes[n2].nodes
                add_edge!(g, n, vertmap[t2])
            end
        end
    end
    nodelabel = [ t.head for (t, id) in e.memo]
    classmap = Dict([ (id,n)  for (n,id) in enumerate(Set([ id.id for (t, id) in e.memo]))])
    nodecolor = [classmap[id.id] for (t, id) in e.memo]
    
    return g, nodelabel, nodecolor
end

function graphplot(e::EGraph) 
    g, nodelabel,nodecolor = graph(e)


    # Generate n maximally distinguishable colors in LCHab space.
    nodefillc = distinguishable_colors(maximum(nodecolor), colorant"blue")
    gplot(g, nodelabel=nodelabel, nodefillc=nodefillc[nodecolor])
end

Example Usage

A simple toy problem is to use equalities like $f^n(a) == a$. What this does is put a loop in the EGraph.

e = EGraph()
a = constant!(e, :a)
f = term!(e, :f)
apply(n, f, x) = n == 0 ? x : apply(n-1,f,f(x))


union!(e, a, apply(6,f,a))
display(graphplot(e))

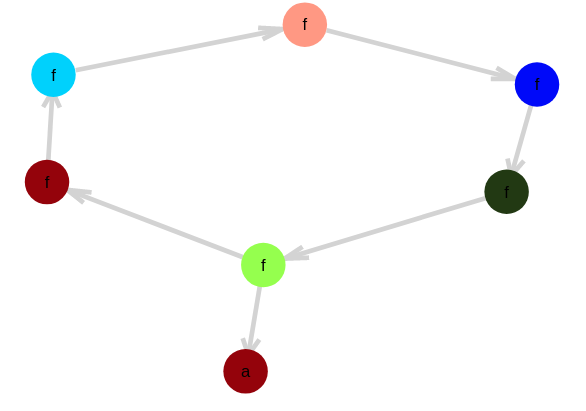
If you think about it, if we assert another equality $f^m(a)==a$, what we’re kind of doing is computing the $gcd(n,m)$. Here the gcd(6,9) = 3.

union!(e, a, apply(9,f,a))
rebuild!(e)
display(graphplot(e))

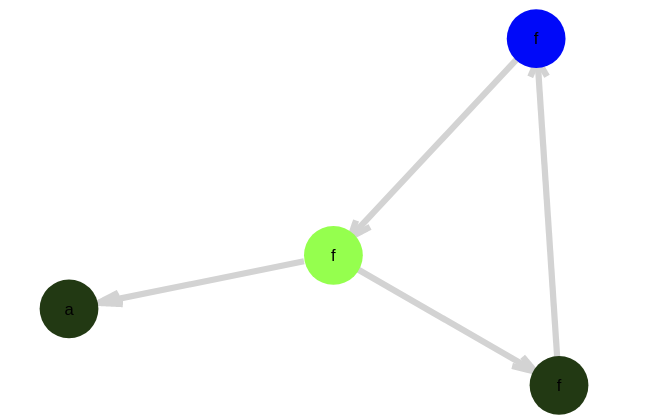
And then if additionally we assert a prime number of applications of f, we reduced the loop of nodes to a single equivalence class

union!(e, a, apply(11,f,a))
rebuild!(e)
display(graphplot(e))

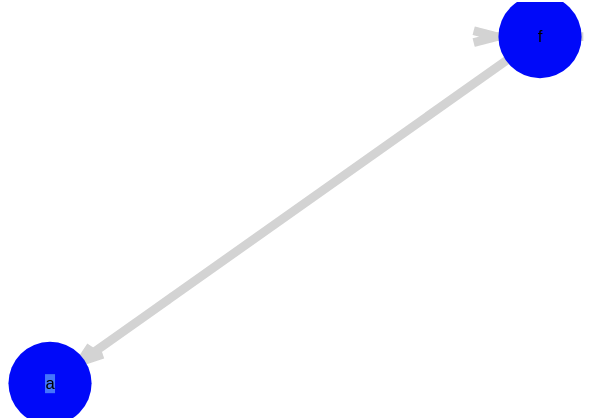
We’ve only just begun. To do anything really fun, we need to implement pattern matching over the E-graph (EMatching).

We’ll see.

Bits and Bobbles

  • I should try just binding to egg. A combo of https://github.com/herbie-fp/egg-herbie and https://github.com/felipenoris/JuliaPackageWithRustDep.jl makes it seem like this shouldn’t be so bad. My implementation is trash compared to egg’s and I haven’t even done pattern matching yet
  • Factoring out the hashcons in the struct definition is like factoring out Fix in recursion schemes
  • Factoring out hash cons is like factoring out the fix for a recursive definition. When you do this, it also opens up the option of memoization, like in fib
  • Unification and union find. If you don’t congruence close, and instead merge recursively down terms, you get a kind of unification. Each equivalence class can only hold variables and terms of the same head for the unification to succeed. This can be checked after unioning everything. I think this is roughly what the MM algorithm does
  • Halfway House E-graph. For a loss of efficiency, you can store a simpler e graph structure that is really is basically a hash cons and union-find smashed together.
  • The models returns by Z3 for a bunch of equalities are basically a serialization of the E graph. Could this be a way to build a rewrite library? You might have to reimplement pattern matching.

References