Well, the time has come once again. I have been spending a decent amount of time thinking about a problem of questionable worth and I need to checkpoint it.

I’ve been trying to embed lambda prolog like features in regular prolog. Prolog implementations have a lot of effort put into them, and a fairly large ecosystem, so there are advantages if this can be achieved.

Lambda prolog has two interrelated aspects to it, extending the horn clause structure to Harrop and allowing higher order unification. I’m attacking the Harrop part first (and I kind of think it’s more important / interesting).

The basic extra features that Harrop clauses offer on top of prolog is the ability to locally assert clauses into the database and the creation of fresh constant when you traverse under pi aka forall binders.

This paper, “A Declarative Alternative to “assert” in Logic Programming”, attacked kind of the same problem. Maybe the addition of continuations to prolog since then changes the solution space though.

Really, if you want these features to work right you should probably just use elpi. But I did discover some useful tidbits, so here we go.

It’s easy right?

Ok, prolog offers dynamic predicates which can be controlled by asserta and retract. Additionally, there is a gensym facility for making fresh constants. Awesome.

This suggests two simple implementations of these features.

impl(D,G) :- asserta(D), G, retract(D).
pi(X,B) :- gensym(fvar,X), B.

No.

`asserta` doesn’t work

There are a 2 problems with using asserta:

Retracting at the right moments
Maintaining connections between the variables in the asserted clauses and in the current env.

What if the goals in between the assert and retract fail? Then the assert will not get cleaned up. What if there are multiple solutions? Then retract gets called too many times.

This is somewhat reminiscent of controlling cleanup of resource usage like file handlers. Prolog offers the setup_call_cleanup/3 for this use case. I don’t think this solution works, since I believe the retract only gets cleaned up once.

The other issue is that assert treats variables as universally quantified, when only some of should be. assert breaks the connection between the logical variables in the term you are asserting and the variables you have in your current goal stack. I don’t know how to recover this behavior easily using assert.

For example, assert(foo(X)), X=a, foo(b) ought to fail if we wanted X to stay connected, because assert(foo(X)) retroactively means assert(foo(a)) under this reading. But assert treats it like the clause foo(X). which says foo is true of everything.

The problem with pi

The problem with pi(X,B) is horrible variable scoping hygiene

It needs the extrude check to prevent the gensym we put into X from escaping out of B.
Copies of the pi share the same X if you use it more than once.
Accidental variable collision pi(X,pi(X,true)) will not do the right thing.

A crucial feature of the proper treatment of these forall fresh variables is the extrude check. In its usage for existentials, a logic variable is supposed to be a lazily filled in concrete ground term. But this ground term should only contain symbols that existed at the time you traversed the ex binder, and hence constants generated by inner pi are not acceptable candidates. This check is similar in some ways to the infamous occurs check in that it is a limitation on unification, really required for logical soundness, and kind of annoying operationally speaking.

Point 3 may seem silly. It’s one of those “well if that hurts, don’t do that” kind of things, but it has bit me.

See Oleg’s related comments on abusing logical variables for lambda binders

Metainterpreter

An good tact is to try to build a metainterpreter.

It is definitely going to be possible to build a lambda prolog metainterpreter in prolog. You can build an interpreter for any language in prolog with enough muscle grease, but the ultimate goal is to remove the interpreter.

It actually isn’t obvious how to write the interpreter correctly though. Nasty scoping issues.

So, what we can do is take the inference rules for Harrop clause’s out of Miller and Nadathur (I love this book) and directly translate them to an interpreter.

One of the things I enjoy about prolog is that it makes inference rules (the horizontal line things) operational. The horizontal bar really is prolog’s :-.

These are right rules that deconstruct goals

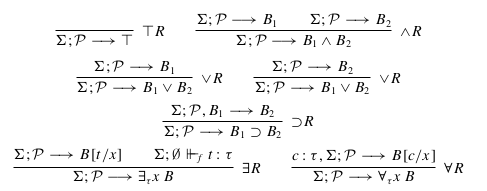
And these are left rules that try to use a focussed clause.

and here is the prolog code

:- use_module(library(yall)).
:- use_module(library(apply)).
:- use_module(library(apply_macros)).
:- initialization(main,main).
:- use_module(library(occurs)).

extrude_check(S,T) :- forall((sub_term(X, T), ground(X), X = fvar(Y)), member(Y,S)). 

right(_,_,true).
right(S,P,and(B1,B2)) :- right(S,P,B1), right(S,P,B2).
right(S,P,or(B1,_B2)) :- right(S,P,B1).
right(S,P,or(_B1,B2)) :- right(S,P,B2).
right(S,P,impl(B1,B2)) :- right(S,[B1|P],B2).
right(S,P,ex(L)) :- call(L,X,G), right(S,P,G), extrude_check(S,X).
right(S,P,all(L)) :- gensym(v,X), call(L,fvar(X),G), right([X|S],P,G).
right(S,P,+A) :- member(D,P), left(S,P,D,A). %decide focuses a program clauses

left(_,_,+A,A).
left(S,P,impl(G,D), A) :- left(S,P,D,A), right(S,P,G).
left(S,P,and(D1,_D2), A) :- left(S,P,D1,A).
left(S,P,and(_D1,D2), A) :- left(S,P,D2,A).
left(S,P,all(L), A) :- call(L,X,D), left(S,P,D,A). 

We use a couple tricks. Instead of pi(X,B), we use a HOAS-like pi(L). L is a goal that can be called with 2 arguments. The first is the instantiation of X, and the second is an output parameter G that will be unified with B with X replaced. We can’t really have L “return” G = B[t/X] because returning isn’t a thing in prolog, so this is what we have to do.

It is a HOAS in the sense we are borrowing prolog’s natural notion of scoping inside a clause for our uses.

We use the prolog lambda library library(yall) as a convenience for building L. The scoping behavior of this library is not great and I have had to use the {} capturing notation. To be safer, you can manually lambda lift the L predicates that go into pi

For the extrude check, since we explicitly introduce the existential variables with ex(L), we can check for scope extrusion after calling L is done. It is possible this is not right, but I’m not sure how else variables could escape their scope.

We have two extra context parameters we thread in the interpreter. One is the signature S which holds gensymed variables so that we can perform the extrude_check. The other is the program context P which holds clauses introduced by impl. They are mostly very passively threaded.

I use the + marker on predicates to make this a “clean” representation rather than a defaulty one.

Implicit Context and Scoped Databases with library(intercept)

Really, to make this interpreter more shallow, the obvious thing to do is look for mechanisms to help us carry implicit contexts.

One option might be Definite Clause Grammars, which can be used to encode stateful computations by modelling the sequence of states as a stream. It’s not that shallow in that then everything we do has to be lifted to DCG land.

We don’t really need state persay to implement this because the context is scoped. This is a subtle idea that is familiar to me from use of the Reader vs State monad. This is the same distinction as that between shadowing let bound variables and actual mutable variables. When you leave the scope, let bound variables come back. Likewise when we leave an impl scope, we restore the old program context.

Another fun option is to use delimited continuations. The “delimited” part of that is referring to a notion of scope. When we need to access the context, we can jump out to a delimitation point and grab it there.

Apparently, library(intercept) is better behaved than general delimited continuations. I think this library implements something very similar to one-shot delimited continuations. Using it looks very much like a throw/catch that can return values back to the throw. This is related to algebraic effects. All these concepts are one big mash.

I found it easiest (necessary?) to mark certain predicates as scoped dynamic by adding a clause that will try to search the current program context. This is similar in spirit to how tabled predicates are marked :- table fib/2. because they need to try searching the table.

This is a simple version that only allows assert of ground facts, and/or logic variables that stay connected to the one’s in the current goal stack.

:- use_module(library(intercept)).
:- initialization(main,main).

% add this clause to mark bar/1 as "scoped dynamic predicate"
bar(X) :- get_ctx(facts(P)), member(D,P), D = bar(X).
% also can have regular global clauses
bar(X) :- biz(X).
bar(c). 

impl(D,G) :- get_ctx(facts(P)), intercept(G, facts(P1), =(P1), [D|P]).
get_ctx(facts(P)) :- catch(send_signal(facts(P)), error(unintercepted_signal(facts(_)),_), P = []).

main(_) :- impl(bar(a), (bar(X), impl(bar(b), bar(Y)))), writeln(X), writeln(Y).

I used the catch handler in get_ctx just to avoid needing a preliminary intercept to iniitiate the program context to []. Maybe this is too cute and unwise.

A different convention of what we store in the context is that we store a lambda representation that when called with the current goal, either fail or succeed. This form is better for more interesting clauses with more interesting variable binding structure. This means converting a clause that looks like

bar(X,Y) :- biz, baz(X,Z).

into a “goal/head-passing” representation

bar1(G) :- G = bar(X,Y), biz, baz(X,Z).

before the clause is able to be store in the clause context. Variables that need to be maintained in connection to the current ones in scope are extra parameters to bar1. For example bar(A,B,G) would be inserted as an entry bar(A,B) in the clause context.

To install this capability into foo/1 it would look like

foo(X) :- send_signal(clauses(P)), member(D,P), call(D,foo(X)).

If I used delimited continuations, a natural design might be to just bounce requests up the delimitation point chain until you find one that works, but that doesn’t work for intercept. We’d then need intercept to return multiple times.

Bits and Bobbles

Could attributed variables do the extrude check?
gensym might be a bad idea. Could carry around an integer in context to represent current free vars in scope
Linearly searching the clause context using member is silly. We could use much better indexing, like some kind of trie. There are readily available facilities
Do I have enough pieces to implement the rule construct from A Declarative Alternative to “assert” in Logic Programming or not?
This blog post was partially prompted by this discussion

Addendum

A thread discussing this post had some interesting points.

One cool example that came up is the drinker’s paradox

The drinker’s paradox is an interesting example because the extrude_check blocks it. The goal is ex x, D(x) → forall y, D(y). Under the proof search reading I am following, first we introduce a logical variable X when we traverse ex, then we scoped assert D(X), then we gensym a fresh y, then we try to resolve D(y) against the database. It unifies X with y, so retroactively, we actually asserted D(y) into the database at the implication step. Great. But now when exiting the ex binder it checks if the term X contains any fresh variables it shouldn’t as the extrude check. X is indeed y now which was not in scope at the time of traversing the ex binder, so this check fails. Hence the goal of the drinker’s paradox fails.

The relationship to the Jens Otten provers (slides patt 2) should have been more obvious to me. The trick of using the occurs_check to implement the extrude check is quite clever. If we make our gensymed fresh constants hold the existentials in context, then the occurs check will fail if those existentials ever get unified to the fresh constant that was no in scope for them. The occurs check makes sure no cyclic terms are made by unfication and can be turned on globally via a flag.

Looking at the implementation of yall, it appears that it works via copy_term implementation. If instead of using yall, I inline those tricks, it can make for an interpreter where the user is less likely to make mistakes adding the {} / variable capturing annotations. I hadn’t realized that copy_term can be used to make shared variables via the pattern copy_term(Shared-T, Shared-T1) where Shared holds a list of the logical variables you want to share with the fresh copy T1

undo/1 may be a way to recover good behavior of assert. Maybe something like impl(D,G) :- assert(D), undo(retract(D)), G, retract(D), undo(assert(D)) ? I am a little skeptical. Blowing the lid off of imperative effects and then trying to plug the leaks sounds like a scary proposition. snapshot also sounds interesting.

Jan suggests looking at XSB which has a notion of a first class clause set. I’m not sure how much this would help semantically speaking. This might be just a drop in more efficient replacement for my P clause list?

“Embedded Implication” and “hypothetical reasoning” are both phrases that seem relevant. see this paper They do a thing that looks like using assert but they pass in the shared variables as a separate argument. Maybe some kind of global variable, or maybe storing an E context like the S or P could work. I did have a version I was threading that, but then I didn’t know why. They’re metainterpreter looks very similar to the one below. The performance numbers look ok compared to their compiled version. Maybe metainterpreter is the way to go.

It is disappointing that it is very easy to miss an accidental logical variable introduction. Marking all of them with ex is the only way to register them. It seems very impossible to know all the variables in scope… Is that true? They are held on a stack probably? In some sense the continuation might have all the currently in scope variables.

@j4n_bur53 has a cleaned up version of my interpreter using some of these trick.

/**
 * Warranty & Liability
 * To the extent permitted by applicable law and unless explicitly
 * otherwise agreed upon, XLOG Technologies AG makes no warranties
 * regarding the provided information. XLOG Technologies AG assumes
 * no liability that any problems might be solved with the information
 * provided by XLOG Technologies AG.
 *
 * Rights & License
 * All industrial property rights regarding the information - copyright
 * and patent rights in particular - are the sole property of XLOG
 * Technologies AG. If the company was not the originator of some
 * excerpts, XLOG Technologies AG has at least obtained the right to
 * reproduce, change and translate the information.
 *
 * Reproduction is restricted to the whole unaltered document. Reproduction
 * of the information is only allowed for non-commercial uses. Selling,
 * giving away or letting of the execution of the library is prohibited.
 * The library can be distributed as part of your applications and libraries
 * for execution provided this comment remains unchanged.
 *
 * Restrictions
 * Only to be distributed with programs that add significant and primary
 * functionality to the library. Not to be distributed with additional
 * software intended to replace any components of the library.
 *
 * Trademarks
 * Jekejeke is a registered trademark of XLOG Technologies AG.
 */

/**
 * See also:
 * https://www.philipzucker.com/harrop-checkpoint/
 */

right(_,_,true) :- !.
right(S,P,(B1,B2)) :- !, right(S,P,B1), right(S,P,B2).
right(S,P,(B1;_B2)) :- !, right(S,P,B1).
right(S,P,(_B1;B2)) :- !, right(S,P,B2).
right(S,P,(B1->B2)) :- !, right(S,[B1|P],B2).
right(S,P,ex(W,L)) :- !,
   copy_term((W,L)-S,(V,R)-S),
   right([V|S],P,R).
right(S,P,all(W,L)) :- !,
   flag('$sk', N, N+1),
   copy_term((W,L)-S,(sk(N,S),R)-S),
   right(S,P,R).
right(S,P,A) :- member(D,P), left(S,P,D,A). %decide focuses a program clauses

left(S,P,(G->D), A) :- !, left(S,P,D,A), right(S,P,G).
left(S,P,(D1,_D2), A) :- !, left(S,P,D1,A).
left(S,P,(_D1,D2), A) :- !, left(S,P,D2,A).
left(S,P,all(W,L), A) :- !,
   copy_term((W,L)-S,(V,R)-S),
   left([V|S],P,R,A).
left(_,_,A,B) :- unify_with_occurs_check(A,B).

Why did I even want this stuff?

hypothetical rewriting / contextual in egglog
guesses in disassembly or decompilation

Junk

A Digression on Different Meanings of Logical Variables

Would adding let to prolog help scoping? let is compatible with first order logic without the complications of higher order logic.

Logical variables mean different things. It’s way too overloaded a concept.

Prolog has some of the worst variable hygiene of any language I know of.

Sometimes a term with a variable represents a ground term that will have something filled in later.

When a query returns a logical variable, it is asserting a universally quantified answer, not an exisentially quantified one. Logical variables are implicitly existentially quantified in goals and universally quantified in answers. Very very different things.

It can also be useful to think of a term with variables in it as representing the set of all ground terms that unify with that term.

It s tempting to attempt to use logic variables to represent lambdas. When you unify the variable, it will subsitute it everywhere just like a lambda right? Very efficient, very cool.

The issue is multiple copies of that lambda get destructively assigned all at once.

See Oleg Kiselyov’s discussion of this

I think it is generally quite unwise to attempt to use one kind of variable for another. Very subtle errors will arise.

Prolog’s forall and pi

The relationship of the lambda prolog pi and the standard forall/2 predicate is interesting. forall/2 can be seen as a bounded forall really and gets into the whole negation as failure business. Whereas pi creates a fresh var, and if you can prove the body given no other properties of this fresh var, the property must be true.

Using the interpreter

main(_) :- 
  P = [
  all([L,T] >> (T = +append([], L, L))),
  all([H,T] >> (T = all([L1, T1] >> 
               (T1 = all([L2,T2] >> 
               (T2 = all([L3, T3] >> 
               (T3 = 
        impl(+append(L1,L2,L3),
             +append( [ H | L1], L2, [H | L3]))))))))))
  ], right([], P, +append([a,D], [c], Z)), writeln(Z),
  right([],[],true), writeln(pass),
  right([],[+a], +a), writeln(pass2),
  right([],[+a,+b], +b), writeln(pass3),
  right([],[all([X,T] >> (T = +foo(X)))],+foo(a)), writeln(pass4)
  , right([], [+append(nil, nil, nil)], +append(nil, nil, nil)) , writeln(pass5)
  , right([], P, +append([], [], X)) , writeln(X), writeln(pass6),

  right([], [], impl(+a,+A)), writeln(A),
  right([], [], impl(and(+a,+b),+b)),
  right([], [], impl(and(+a,+b),+b)),
  right([], [], all([Q,G] >> (G = impl(+foo(Q),+foo(Q))))),
  %\+ right([], [], all([Q,G] >> (G = impl(+foo(Q),+foo(a))))),
  right([], [], all({F}/[Q1,G1] >> (G1 = impl(+foo(Q1),+foo(F))))), writeln(F),

  %right([], [], ex([H1,J1] >> (J1 = impl(+foo(H1),+foo(H1))))),
  writeln(pass7),!,
  %right([], [], ex([H2,J2] >> (J2 = all({H2} / [Q2,G2] >> (G2 = impl(+foo(Q2),+foo(H2))))))),
  writeln(pass8),
  right([],[],ex(foo)),
  writeln(pass9),
  query(Q7),
  right([],[],Q7)





  %right([],[],[], append(nil,nil,nil)), print(passed)
.

Direct opening and closing

Could go for a regular locally nameless encoding rather than trying to use HOAS. make open and close predicates.

Naw, why even seaprate out the args? Maybe better indexing, but screw it for now. assert_chr(foo(Args)). I might be building a prolog (meta?) interpreter in chr.

locally nameless encoding of exists. do opening with X. no copy_term of program clauses.

open(evar(N),N,X,X).
open(evar(M),N,X,evar(M)) :- dif(N,M).

close(). Hmm. Maybe we never need to close.

mi(S, P, all(B)) :- gensym(X), open(B,0,fvar(X), B1), mi([fvar(X)|S], P, B1).
mi(S, P, ex(B)) :- open(B,0,X,B1), mi(S,P,B1), extrude_check(S,X).
mi(S, P, D => G) :- mi(S,[D|P], G).
mi(S, P, +G) :- 
mi(S, P, +G) :- call(G). %native call

% de bruijn the named rep. This is close I guess.
bruijn(T,T1) :- number_var(T, T2), bruijn([], T2,T1)
bruijn(Vars, var(N), var(I)) :- index(Vars, N, I).
bruijn(Vars, ex(X,B), ex(T1)) :- bruijn([X|Vars], B, T1). 

mi(Sig, Env, Prog, all(B)) :- gensym(X), mi([X | Sig], [X | Env], Prog, B).
% if I distinguish avar(N) from evar(N), Sig is already an Env

mi(Sig, Env, Prog, var(N)) :- lookup(N,Env,V). % and V goes where?
mi(Sig, Env, Prog, +G ) :- subst(G,Env,Sig).

% do subsitution lazily instead of eagerly.

normalization by evaluation. Hmm. What if I did use the lambda library https://www.swi-prolog.org/pldoc/man?section=yall

all(L) :- gensym(X), call(L, fvar(X)).
ex(L) :- call(L, Y), extrude_check(Y).
impl(D,G) :-  call(asserta(D), G) -> retract(D) ; retract(D), fail. 
% ok but asserta loses track of current unification variables.
% also problem if G produces multiple answers?
% label_vars(D,D1). asserta(D :- subst(D1, )
% pack it, then unpack it on other side.
% number_vars, term_variables
% https://www.cs.cmu.edu/~fp/papers/ilps91.pdf mentions the assert retract encoding. Mentions that variables are nasty.

right(_,_,true).
right(S,P,and(B1,B2)) :- right(S,P,B1), right(S,P,B2).
right(S,P,or(B1,_B2)) :- right(S,P,B1).
right(S,P,or(_B1,B2)) :- right(S,P,B2).
right(S,P,impl(B1,B2)) :- right(S,[B1|P], B2).
right(S,P,ex(_X,B)) :- right(S,P,B). % maybe
right(S,P,all(X,B)) :- gensym(X), right([X|S],P,B). % maybe
right(S,P,+A) :- member(D,P), left(S,P,D,A). %decide

% alternate name: clause deonstruct, focused.
left(_,_,A,A).
left(S,P,impl(G,D), A) :- left(S,P,D,A), right(S,P,G).
left(S,P,and(D1,_D2), A) :- left(S,P,D1,A).
left(S,P,and(_D1,D2), A) :- left(S,P,D2,A).
left(S,P,all(_X,D), A) :- left(S,P,D,A). % maybe

Before unify throw signal (attrbuted var). WHy this is wrong: Generally, trying to use the wrong kind of variable is a road strife with peril.

When we use P, we destroy the universal quantifications within. If we copy, we destroy the connection to the existential variables. This is also one of the problems of using asserta. copy_term allows you to add variables to be renamed, but not the ones to be shared. This is the opposite of he behavior we want

It is somewhat natural to expect that lambda terms might be useful. https://www.swi-prolog.org/pldoc/man?section=yall https://www.swi-prolog.org/pack/list?p=lambda https://swi-prolog.discourse.group/t/yall-lambda-arguments-visibility/5112/2 This example is evidence that the implementation of yall may not scope as lambdas should.

Let us go under the (quite possibly faulty) assumption that the story on lambdas is clear in prolog. One can manually lambda lift, defunctionalize, closure convert if you want to.

Lambda’s in yall only produce goals, so far as I can tell. So if you want them to produce terms, that needs to come in as another paramter by convention. This feels a bit like continuation passing or output parameter passing.

:- use_module(library(yall)).
:- use_module(library(apply)).
:- use_module(library(apply_macros)).
:- initialization(main,main).
:- use_module(library(occurs)).

extrude_check(S,T) :- writeln([ex_check, S, T]), forall((sub_term(X, T), ground(X), X = fvar(Y)), member(Y,S)). 

right(_,_,true).
right(S,P,and(B1,B2)) :- right(S,P,B1), right(S,P,B2).
right(S,P,or(B1,_B2)) :- right(S,P,B1).
right(S,P,or(_B1,B2)) :- right(S,P,B2).
right(S,P,impl(B1,B2)) :- right(S,[B1|P],B2).
right(S,P,ex(L)) :- call(L,X,G), right(S,P,G), writeln([ex,X]), extrude_check(S,X).
right(S,P,all(L)) :- writeln(all), gensym(v,X), call(L,fvar(X),G), right([X|S],P,G), writeln([exit_all, G]).
right(S,P,+A) :- member(D,P), writeln([pick,P, D,A]), left(S,P,D,A), writeln([D,A]). %decide

% alternate name: clause deonstruct, focused.
left(_,_,+A,A).
left(S,P,impl(G,D), A) :- left(S,P,D,A), right(S,P,G).
left(S,P,and(D1,_D2), A) :- left(S,P,D1,A).
left(S,P,and(_D1,D2), A) :- left(S,P,D2,A).
left(S,P,all(L), A) :- call(L,X,D), left(S,P,D,A). % maybe


%main(_) :- P = [
%  all( [J, T] >> T = impl(all([X,T1] >> T1 = impl(and(bug(x), in(x,J)), dead(x)), sterile(J))),
%  all( [B, T] >> T = impl(ex([J,T1] >> T1 = and(headed(J), and(in(B,J), bug(B)) ) , dead(B))),
%  heated(j) ]


foo(E,G) :- G = all(bar(E)).
bar(E,X,G) :- G = impl(+foo(X), +foo(E)). 
% ;re
query(Q) :- Q = ex([H2,J2] >> (J2 = all({H2} / [Q2,G2] >> (G2 = impl(+foo(Q2),+foo(H2)))))).

main(_) :- 
  P = [
  all([L,T] >> (T = +append([], L, L))),
  all([H,T] >> (T = all([L1, T1] >> 
               (T1 = all([L2,T2] >> 
               (T2 = all([L3, T3] >> 
               (T3 = 
        impl(+append(L1,L2,L3),
             +append( [ H | L1], L2, [H | L3]))))))))))
  ], right([], P, +append([a,D], [c], Z)), writeln(Z),
  right([],[],true), writeln(pass),
  right([],[+a], +a), writeln(pass2),
  right([],[+a,+b], +b), writeln(pass3),
  right([],[all([X,T] >> (T = +foo(X)))],+foo(a)), writeln(pass4)
  , right([], [+append(nil, nil, nil)], +append(nil, nil, nil)) , writeln(pass5)
  , right([], P, +append([], [], X)) , writeln(X), writeln(pass6),

  right([], [], impl(+a,+A)), writeln(A),
  right([], [], impl(and(+a,+b),+b)),
  right([], [], impl(and(+a,+b),+b)),
  right([], [], all([Q,G] >> (G = impl(+foo(Q),+foo(Q))))),
  %\+ right([], [], all([Q,G] >> (G = impl(+foo(Q),+foo(a))))),
  right([], [], all({F}/[Q1,G1] >> (G1 = impl(+foo(Q1),+foo(F))))), writeln(F),

  %right([], [], ex([H1,J1] >> (J1 = impl(+foo(H1),+foo(H1))))),
  writeln(pass7),!,
  %right([], [], ex([H2,J2] >> (J2 = all({H2} / [Q2,G2] >> (G2 = impl(+foo(Q2),+foo(H2))))))),
  writeln(pass8),
  right([],[],ex(foo)),
  writeln(pass9),
  query(Q7),
  right([],[],Q7)





  %right([],[],[], append(nil,nil,nil)), print(passed)
.

We could also implement scoping the usual way, not trying to pull a fast one by reusing prolog mechanisms. de bruijn indices or locally nameless This brings it’s own peril. We are treated prolog as a functional or imperative language here. Oleg has an example where he uses pure constructs. If we want to make this generic ndexing dif/2

:- use_module(library(reif)).
:- use_module(library(terms)).
:- use_module(library(clpfd)).
:- initialization(main,main).
open_(X,N,T,T1) :- if_(T = lam(B), 
                      (N1 #= N + 1, T1=lam(T2), open_(X,N1,B, T2)) ,
                   if_( T = var(N), 
                       T1 = X,
                   mapargs(open_(X,N), T, T1) % https://www.swi-prolog.org/pldoc/doc_for?object=mapargs/3
                   )).
%close() maybe unecesaary?
main(_) :- writeln(hi), open_(a, 0, lam(var(1)), T), writeln(T).

We don’t need to open persay, since we mostly/entirely just need evaluation? It’s the same as open except doing it eagerly vs lazily / batching the traversal.

right(T1 = T2) --> {unify(T1,T2)}.
eval(S,E,evar(N), V) :- lookup(E,N,V).
eval(S,E,avar(N), V) :- lookup(S,N,V).
eval(S, E, F, R) :- 
unify(S,E,T1,T2) :-
unify(S,E,apply(F,Args), )

% hmm. keeeping E and S vars on same stack is useful because that says what is in scope

We still have a scope extrusion check. An exmample: ???? Existentials should really be being filled in with terms that exist at the time that binder is being opened. The unfication variable is a standin, delaying picking a term so that we can deduce at it should have been, but it is not protected from unifying with forall quantified variables that didn’t exist at the time of it’s creation. These would not have been legitimate concrete terms

By analogy with the occurs_check, we might choose to just not worry about this and hope for some kind of systems magic flag to come along later. Attributed variables might also enable pushing unifiation The interpreter could also insist on treating = specially. It is difficult to avoid accidentally using native prolog unfication both in the interpreter, but also in the interpretted programs.

term_lam(X \ B) :- [G|X] \ (G = B). % does this make sense? Fishy. term_lam = \\ notation

So a natural question is how can we make this interpreter shallower? We are reusing prolog’s search mechanisms and unification mechanisms. So that’s nice.

Implication is sticky though. One might be tempted to use asserta which make dynamic databases. Naive use of this is not right

asserta considers all unification variables to be universals. It breaks the correlation of the program database with the goal
retracting the implication once you leave the scope of it is tricky. Yes retract exists. But it is not clear to me

assert and retract are manipulating a global database store. This is a leaky abstraction and somewhat doomed to failure IMO. Imagine trying to implement function calls using a global memory. Ok I guess you could do it by maintaining your own stack.

By analogy with file handles, we may think some kind of bracketing expression may help. setup_call_cleanup(asserta(D), G, retract(D)) https://www.swi-prolog.org/pldoc/doc_for?object=setup_call_cleanup/3 No. This doesn’t retract at the right point. The search may exit the implication but then return to it on backtracking. This doesn’t retract until G won’t be called anymore.

Ok, well perhaps we never call retract, but instead key on an identifier of what branch we are in. And to deal with the sharing problem, we could replace all E vars in the program clause with keys that access them from a store. It really feels like we’re plugging up hole after hole on a leaky ship.

DCGs can be used to clean up the state carrying a bit, since so may rules do not involve state. https://www.swi-prolog.org/pack/list?p=edcg https://www.metalevel.at/prolog/dcg

:- use_module(library(yall)).
:- use_module(library(apply)).
:- use_module(library(apply_macros)).

right(true).
right(and(B1,B2)) --> right(B1), right(B2).
right(or(B1,_B2)) --> right(B1).
right(or(_B1,B2)) --> right(B2).
right(impl(B1,B2)), [s(_,_,P)] --> [s(_,_,[B1|P])], right(B2).
right(ex(L)), [s(_,E,_)] --> [s(_,[X|E],_)], {call(L,X,G)}, right(S,P,[X|E],G).
right(all(L)), [s(S,_,_)] --> [s([X|S],_,_)], {gensym(X), call(L,X,G)}, right([X|S],P,E,G).
right(+A) --> member(D,P), left(D,A). %decide

left(A,A).
left(impl(G,D), A) --> left(D,A), right(G).
left(and(D1,_D2), A) --> left(D1,A).
left(and(_D1,D2), A) --> left(D2,A).
left(all(L), A) --> {call(L,X,D)}, left(D,A).

Higher order unification is a separate issue. If we are already overloading unification, it is probably not that hard to treat. Miller pattern unification is a subcase of higher order unification that is easy. The idea is to restrict higher order unification to it’s bones.

:- use_module(library(intercept)).
:- initialization(main,main).

%https://www.swi-prolog.org/pldoc/man?section=intercept

%right(+A) :- send_signal(goal(A)).
% hmm, so that send signal is still in scope of the current intercept it seems like?
%right(impl(D,G)) :- intercept(right(G),goal(A), (writeln(A), D=A;send_signal(goal(A)))).

% implicit contxt being parlayed.
left(D,A) :- D = A.
right(+A) :- send_signal(prog(P)), member(D,P), left(D,A). 
right(impl(D,G)) :- send_signal(prog(P)), intercept(right(G), prog(P1), P1 = [D | P]).

run(G) :-  intercept(right(G), prog([]), true).
 % intercept(right(G),goal(A), (writeln(A), D=A)).
main(_) :-  intercept(send_signal(x), X, writeln(X)),
            %intercept((right(impl(foo(c), impl(foo(b), +foo(A)))), writeln(A)), prog([]), true).
            run(right(impl(foo(c), impl(foo(b), +foo(A))))), writeln(A).

So these techniques enable implicit context in different ways. Could receive database per head symbol

:- use_module(library(intercept)).
:- use_module(library(yall)).
:- use_module(library(apply)).
:- initialization(main,main).

biz(X) :- get_ctx(facts(P)), member(D,P), D = biz(X). % for non unversal facts this works. call(D,bar(X))
%biz(X) :- X = foo.

% hmm. I want to reenter the continuation mutiple times though? Is that ok?
% ok, so if I just send back the 


bar(X) :- get_ctx(facts(P)), member(D,P), D = bar(X). % for non unversal facts this works. call(D,bar(X))

bar(X) :- get_ctx(clauses(P)), writeln(P), writeln(X), member(D,P), call(D,bar(X)). % for non unversal facts this works. call(D,bar(X))


% bar(a).


% essentially, reader monad

foo(X) :- send_signal(clauses(P)), member(D,P), call(D,foo(X)).

% mayb send_silent_signal is useful here
% or perhaps catch the error of a missing prog(P).
% use intercept/4 just to make sure variables in P don't get screwed up?
%impl(D,G) :- get_ctx(facts(P)), intercept(G, facts(P1), P1=[D|P]).

impl(D,G) :- get_ctx(facts(P)), intercept(G, facts(P1), =(P1), [D|P]).

climpl(D,G) :- get_ctx(clauses(P)), intercept(G, clauses(P1), =(P1), [D|P]).


get_ctx(facts(P)) :- catch(send_signal(facts(P)), error(unintercepted_signal(facts(_4104)),_4096), P = []).
get_ctx(clauses(P)) :- catch(send_signal(clauses(P)), error(unintercepted_signal(clauses(_4104)),_4096), P = []).

% could maintan seprate lists per functor, but what's the point?
setup_db(G) :- intercept(G,prog(P),P=[]).

buz :- writeln(ap), bar(a), send_signal(facts(P)), writeln([facts,P]), bar(b), writeln(succed_b).

bar_clause(X, G) :- G = bar(X).
biz_clause(G) :- G = bar(X), writeln(X), biz(X).
main(_) :- 
  % yes it traverses to the outer intercept
 %intercept(intercept(send_signal(foo), bar, writeln(bar)), foo, writeln(foo)),
% setup_db((
  %impl(bar(b), impl(bar(c), bar(A))), A \= c, writeln(A), bar(a),

  % \+ impl(bar(_F), (bar(a), bar(b))) % should fail because F needs to be a and b
  %, climpl([G] >> G = bar(a), bar(a))
  %, climpl([G] >> G = bar(a), bar(a))
  %, climpl(=(bar(a)), bar(a)) % this is nice. What if I wanted a body though?
  %, climpl([G] >> (G = bar(X), biz(X)), impl(biz(a), bar(a)))
   climpl(biz_clause, bar(a)) % impl blocks climpl. Hmm. So non interferencing signals don't bubble.
   % Do I need to do  if_( = facts(), P1 = P(),  send_signal()) explicit signal repropgation?
   % intercept(G, Signal, Signal = fact(P) -> doit ; send_signal(Signal))
   % seems very non compostional to require this. Can this be right?
   % Also could use [fact(), clause(), fact()] rep of P
   % or implement impl(D,G) :- climpl(=(D), G). 


  .
% )).
 %intercept((biz(X), send_signal(bar)), bar, X=bar), writeln(X).

% exists is uninterestnig except for scope check.
%pi(L) :- gensym(fvar,X), call(L,X).
pi(L) :- send_signal(fvar(N)), N1 #= N + 1, intercept(call(L, fvar(N1)), fvar(N1), true).

% This seems kind of useful for abductive logic programming. Maybe they have soome tricks?

% more point free combinator tricks rather than using []
% That will be less error prone.

:- use_module(library(intercept)).
:- initialization(main,main).

% add this clause to mark bar/1 as "scoped dynamic predicate"
bar(X) :- get_ctx(facts(P)), member(D,P), D = bar(X).
% also can have regular global clauses
bar(X) :- biz(X).
bar(c). 

impl(D,G) :- get_ctx(facts(P)), intercept(G, facts(P1), =(P1), [D|P]).
get_ctx(facts(P)) :- catch(send_signal(facts(P)), error(unintercepted_signal(facts(_)),_), P = []).

main(_) :- impl(bar(a), (bar(X), impl(bar(b), bar(Y)))), writeln(X), writeln(Y).


% no it does pass signals through.

%main(_) :- intercept(intercept(send_signal(foo(X)), bar(X), writeln(bar)), foo(X), writeln(foo)).

They don’t cover (maybe) the problem of keeping universal variables universal but existentials linked

%:- initialization(main,main).

right(+A) :- shift(goal(A)).
right(impl(D,G)) :- reset(right(G), goal(A), Cont), 
  (Cont == 0 ->
  true;
  (A=D ; shift(goal(A))), call(Cont)).

main(_) :-  reset(right(impl(foo(c), impl(foo(b), +foo(A)))), goal(_), Cont), 
(Cont == 0 -> writeln(A) ; fail).