There are generalizations of our concept of number that are not considered bothersome because they are so darn useful.

It has been a revelation to me to see that the Ordinals (up to $\epsilon_0$), a supposedly “infinite” thing, are completely representable and their arithmetic is perfectly computable by any measure.

Step by step we can look at some other things people already accept and see they aren’t so weird.

  • Quaternions https://en.wikipedia.org/wiki/Quaternion are pragmatically useful for calculations about rotations in 3D space. They have non commutative multiplication, kind of like the vector cross product (historically precedes the concept of cross product actually). We accept quaternions as computable and reasonable.
  • Floats https://en.wikipedia.org/wiki/Floating-point_arithmetic already have bit patterns to represent infinity, -infinity. We accept them as computable and reasonable even if we don’t always actually know what floats are up to. Kind of a trojan horse for bizarre behavior.
  • Polynomials can be represented as lists of coefficients. We accept them and their arithmetic as computable and reasonable.

Once you accept all of these, it doesn’t seem like you have much ground left to object to the ordinals (up to $\epsilon_0$) as a reasonable thing.

Complex Numbers and Quaternions

The complex numbers are completely accepted. They can be visualized as positions in the two dimension complex plane. Likewise, they can be represented ion a computer as pairs/structs of real numbers.

Python has them built in

(1 + 3j)*(4 + 5j)

(-11+17j)

But to drive the point home you can write your own on tuples.

def lit(s):
    return (s, 0.0)
def add(c1,c2):
    return (c1[0]+c2[0], c1[1]+c2[1])
def mul(c1,c2):
    return (c1[0]*c2[0]-c1[1]*c2[1], c1[0]*c2[1]+c1[1]*c2[0])
j = (0.0, 1.0)
one = lit(1.0)
mul(add(lit(1.0), mul(lit(3.0), j)), add(lit(4.0), mul(lit(5.0), j)))

(-11.0, 17.0)

A slightly more exotic but related thing is quaternions https://en.wikipedia.org/wiki/Quaternion. Quaternions in some respects generalize the complex numbers by having 3 possible axes of imaginary components. These number do not have commutative multiplication.

from dataclasses import dataclass
@dataclass
class Quat():
    a:float
    i:float
    j:float
    k:float
    def __add__(self, other):
        return Quat(self.a+other.a, self.i+other.i, self.j+other.j, self.k+other.k)
    def __mul__(self, other):
        return Quat(self.a*other.a-self.i*other.i-self.j*other.j-self.k*other.k,
                          self.a*other.i+self.i*other.a+self.j*other.k-self.k*other.j,
                          self.a*other.j-self.i*other.k+self.j*other.a+self.k*other.i,
                          self.a*other.k+self.i*other.j-self.j*other.i+self.k*other.a)

I = Quat(0,1,0,0)
J = Quat(0,0,1,0)
K = Quat(0,0,0,1)
assert I*J != J*I # noncommutative
(I + J) * (I + I + K)

Quat(a=-2, i=1, j=-1, k=-2)

Familiar Infinities

The aspect that the ordinals are talking about infinity isn’t that odd. Simple notions of infinity can be accounted for by just reserving a Tag or bit patterns.

The built in floating point we all use already have special bit patterns for positive and negative infinity and not a number.

These infinities are special absorbing tags that can be useful for default values in dynamic programming or for limits. The slightly more mathy version of this is the extended reals. https://en.wikipedia.org/wiki/Extended_real_number_line .

There isn’t really anything too deep going on here. Mostly just a cute little wrapper/notation to clean up definitions and these infinities have little relation to the ordinals. Still, it conceptually opens the door for us to talk about “infinite” things in finite ways we can computably manipulate.

print(float("inf") + 10.0)
print(8 * float("-inf"))
print(10000000 < float("inf"))

inf
-inf
True

Nat Coefficient Polynomials

Polynomials are another number like thing with implementable arithmetic operations. Sympy can do it for example.

import sympy as sp
x = sp.symbols('x')
sp.poly((1 + 2*x**2)*(2*x + 1))

$\displaystyle \operatorname{Poly}{\left( 4 x^{3} + 2 x^{2} + 2 x + 1, x, domain=\mathbb{Z} \right)}$

But let’s do it ourselves to work our way up to ordinals, which we will represent as polynomials in $\omega$, the first infinite ordinal.

This is a slightly crazy looking way to write polynomials with coefficients that are natural numbers. We can expand any polynomial to have coefficient 1, as $x^n + x^n + x^n + … x^0 + x^0$. For example $(1 + 2x^2)(2x + 1)$ is normalized as $x^3 + x^3 + x^3 + x^3 + x^2 + x^2 + x^1 + x^1 + x^0$ which in python can be represented (3,3,3,3,2,2,1,1,0).

We can implement such a polynomial as a sorted tuple of coefficients.

from dataclasses import dataclass
@dataclass
class Poly():
    coeff: tuple[int,...]
    def __init__(self, coeff):
        self.coeff = tuple(sorted(coeff, reverse=True))
    def __add__(self, other):
        return Poly(self.coeff + other.coeff)
    def __mul__(self, other):
        # reduction to monomial multiplication
        return Poly([c1+c2 for c1 in self.coeff for c2 in other.coeff])
    def from_int(n):
        return Poly([0]*n)
    
zero = Poly([])
one = Poly([0])
assert one == Poly.from_int(1)
two = one + one
assert two == Poly([0,0]) == Poly.from_int(2)
x = Poly([1])
x2 = x*x
assert x2 == Poly([2])

(one + two * x2)*(two * x + one)


Poly(coeff=(3, 3, 3, 3, 2, 2, 1, 1, 0))

We could represent this differently as a dictionary pointing from the exponent to the count of that monomial and in fact that probably would be my first impulse. It is this form which generalizes to polynomials with more interesting coefficients like integers, reals, complex numbers etc.

Note that we can also consider this to be a multiset of our monomials. A sorted list of elements is a canonical form of a multiset https://www.philipzucker.com/hashing-modulo/

from collections import Counter
Counter(((one + two * x2)*(two * x + one)).coeff)

Counter({3: 4, 2: 2, 1: 2, 0: 1})

Ordinals

The ordinals have something called the Cantor normal form https://en.wikipedia.org/wiki/Ordinal_arithmetic#Cantor_normal_form , which is a “polynomial” expansion in the infinite ordinal $\omega$. The caveat here is that the powers are now not just restricted to natural numbers but ordinals.

We can represent ordinals up to $\omega^\omega$ using the same form unary nat polynomials as previously, but now we need to note that arithmetic of ordinals has some strange laws.

For the subset of the ordinals that are natural numbers, everything works like it used to, but multiplication of ordinals is non commutative in general. This is like quaternions. However, addition is also non commutative. And only one direction of distributivity works. Still, there are enough laws for us to compute with polynomials of powers of $\omega$.

  • \((a + b) + c = a + (b + c)\) addition associativity. This dignifies us using flat tuples for a summation of omega monomials

  • \(a(bc) = (ab)c\) multiplication associativity

  • \(\omega^n + \omega^m = \omega^m\) if \(n < m\). In other words, big powers of omega eat smaller omegas to the left. This let’s us canonically compress a sequence of omega powers

  • \(a(b + c) = ab + ac\) left distributivity (BUT NOT RIGHT). This gives us a strategy of breaking down the right term, and multiplying by monomials on the right.

We do not have a property that tells us how to deal with the broken down $(\omega^a + \omega^b + … ) \omega^n $ yet.

  • $ x* 0 = 0 $
  • $ x * 1 = x $
  • If $n > 1$ then multiplying on the right by a monomial grabs out the highest power of $\omega$ and deletes the rests \((\omega^a + \omega^b + ...) \omega^n = \omega^{a + n}\)

With that, we’re ready to go.

from dataclasses import dataclass
import itertools
@dataclass
class OrdPoly():
    coeff: tuple[int,...]
    def __init__(self, coeff):
        self.coeff = tuple(sorted(coeff, reverse=True))
    def __add__(self, other):
        # `other` eats the dominated tail of self 
        if other.is_zero(): # x + 0 = x
            return self
        biggest = other.coeff[0]
        return OrdPoly(tuple(x for x in self.coeff if x >= biggest) + other.coeff)
        # takewhile might be lightly more efficient.
        #return OrdPoly(itertools.takewhile(lambda x: compare(x, ys[0]) >= 0, xs)) + ys)
    def mono_mul(self, n : int) -> 'OrdPoly':
        if self.is_zero(): # 0 * w^n = 0
            return self
        elif n == 0: # multiplication by 1 = w^0,  
            return self # x * 1 = x
        else:
            return OrdPoly([self.coeff[0] + n]) # 
    def __mul__(self, other):
        # reduction to right monomial multiplication
        return sum([self.mono_mul(n) for n in other.coeff], start=OrdPoly.zero()) # note sum is doing ordinal summation, not integer.
    def from_int(n : int):
        return Poly([0]*n)
    def zero():
        return OrdPoly([])
    def is_zero(self):
        return len(self.coeff) == 0

zero = OrdPoly.zero()
one = OrdPoly([0])
w = OrdPoly([1])
w2 = w*w
assert w2 == OrdPoly([2])
assert one + w == w
assert w + one == OrdPoly([1,0])

(one + w2)*(w + one)


OrdPoly(coeff=(3, 2))

There is actually a python package that implements it’s own ordinals https://github.com/ajcr/transfinite, an interesting read https://github.com/ajcr/transfinite/blob/master/transfinite/ordinal.py . This agrees with our calculation

from transfinite import w
(1 + w*w)*(w + 1)

$\omega^{3}+\omega^{2}$

$\epsilon_0$ by Recursion

To go all the way up to $\epsilon_0$, which is a depending on your perspective is a very large number or quite small ordinal, we need to turn this thing recursive. The exponents now need to be ordinals themselves instead of just natural numbers. This is surprisingly easy to do.

A cute trick here is python uses lexicographic ordering on tuples. Because of our sorted unary representation of multisets, this ordering also gets us the ordinal/multiset ordering.

@dataclass(order=True)
class Ord():
    coeff: tuple['Ord',...]
    def __init__(self, coeff):
        self.coeff = tuple(sorted(coeff, reverse=True))
    def __add__(self, other):
        # `other` eats the dominated tail of self 
        if other.is_zero(): # x + 0 = x
            return self
        biggest = other.coeff[0]
        return Ord(tuple(x for x in self.coeff if x >= biggest) + other.coeff)
    def mono_mul(self, n : 'Ord'):
        if self.is_zero():
            return Ord.zero()
        else:
            return Ord.omega(self.coeff[0] + n) 
    def __mul__(self, other):
        # reduction to monomial multiplication
        return sum([self.mono_mul(n) for n in other.coeff], start=Ord.zero()) # note sum is doing ordinal summation, not integer summation.
    def omega(n : 'Ord') -> 'Ord':
        return Ord([n])
    def from_int(n : int):
        return Ord([Ord.zero()]*n)
    def zero():
        return Ord([])
    def is_zero(self):
        return len(self.coeff) == 0
    def __repr__(self):
        if len(self.coeff) == 0:
            return "0"
        return " + ".join(f"w^({repr(x)})" for x in self.coeff)

assert Ord.from_int(0) == Ord.zero()
assert Ord.from_int(1) == Ord.omega(Ord.from_int(0))
w = Ord.omega(Ord.from_int(1))
assert w + w*w == w*w
assert w + Ord.zero() == w
assert Ord.zero() + w == w

Bits and Bobbles

There is also ordinal exponentiation

I don’t really know how to work with the definition of ordinal arithmetic in terms of successors and limits.

Surreals. Use transfinite package. A little calculus?

the difference between w as a set and the ordinal w itself. Abstract domain or intervals. Intervals. Actually implementing an omega cpo.

Ordinal addition and multiplication can be visualized. Ordinal addition is concatenation. You can see the $2 + \omega = \omega$ can absorb the 2.

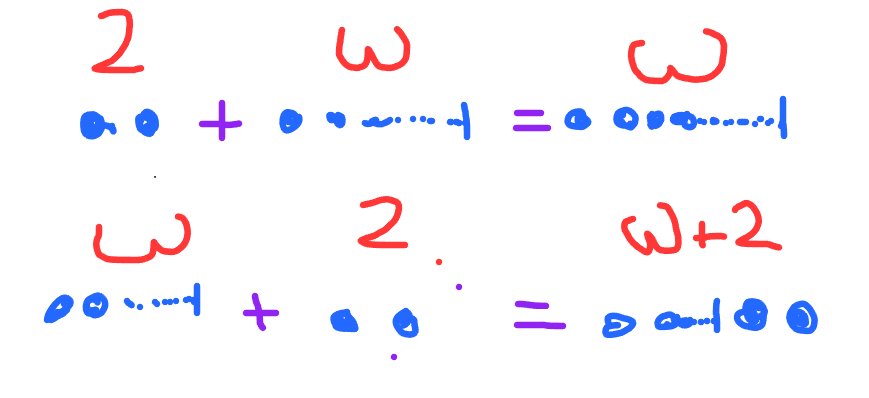
Ordinal multiplication is turning every element of the left into a copy of the right. To me, this is reminiscent of how kronecker product kron(A,B) makes an A-sized block matrix of copies of B.

I saw Graham screwing up his face when I quizzed him about ordinal arithmetic and I realized he was calculating or visualizing something. He was visualizing this concatenation process.

These aren’t just operations on ordinals. You can concatenate and product any orderings, not just total well founded ones.

The ordinals are representing hereditary multisets. This is multisets of multisets of multisets… The analog of sets of sets of sets is hereditary sets. https://www.philipzucker.com/finiteset/

Ordinals are one way of talking about termination. https://podcasters.spotify.com/pod/show/cody-roux/episodes/Ordinals-I-e2d40io

https://en.wikipedia.org/wiki/Ordinal_analysis#Examples

Ordinals

The ordinals are one possible generalization of the natural numbers to include infinities. In particular, they focus on the property of the naturals that they are totally ordered and that counting down with naturals always has to stop/terminate. In more technical words, the inequality relation on naturals is a well order.

Ordinals are reasonable mathematical model of the concept of enumeration extended to the infinite. Cardinals are a reasonable extension of the notion of size. That these do not coincide in the infinite as they do in the finite is somewhat surprising, but the infinite is a surprising place.

https://en.wikipedia.org/wiki/Ordinal_number https://en.wikipedia.org/wiki/Well-order https://en.wikipedia.org/wiki/Well-founded_relation

The ordinals are sometimes constructed in the context of set theory as transitive sets. This construction is useful but also somewhat artificial. The same construction is how the naturals are encoded in set theory. This construction is not at all the source of intuition or the platonic realness of the naturals, and we shouldn’t expect it to be for the ordinals either.

We should also keep in mind the complexity which is hidden by python having a built in integer type. Computers implement arithemtic using binary, in other words by representing numbers as a sum of powers of 2. For example, 9 = 1*2^0 + 0*2^1 + 0*2^2 + 1*2^3 = 0b1001. If we had to spell this out we could represent ordinary numbers as tuples of booleans. Arithmetic is perfectly computable, but kind of a pain.

The cantor normal form of ordinals can be thought of as a “base $\omega$” expansion of an ordinal, so we should anticipate at least as much complication as binary expansions of . A difference is that instead of having powers of the base be whole numbers, we extend powers to also be ordinals themselves (since ordinals are one possible extension of whole numbers).

Like many things, there is a package available for python for the ordinals up to $\epsilon_0$

# generating a multiplication and addition table
from transfinite import w
import pandas as pd
add = {}
mul = {}

items = {0,1,w}
for i in range(2):
    for a in items:
        for b in items:
            add[(a,b)] = a + b
            mul[(a,b)] = a * b
    items = set(add.values()).union(set(mul.values()))

add_df = pd.DataFrame(dtype=object)
for (a, b), result in sorted(add.items()):
    add_df.at[a, b] = result
display(add_df)

mul_df = pd.DataFrame(dtype=object)
for (a, b), result in sorted(mul.items()):
    mul_df.at[a, b] = result
display(mul_df)

But it may comfort us and is interesting to me to talk about how to implement such a thing.

A subcase is how to we represent polynomials?

zero = {}
one = {0 : 1.0}
x = {1 : 1.0}
def add(p,q):
    p = p.copy()
    for k,v in q.items():
        p[k] = p.get(k, 0.0) + v
def mul(p,q):

Addition is associative. We can treat a sum expression as a list of terms. Bigger powers of $\omega$ eat smaller powers on the left.

zero = []
one = [(0,1)] # power, coefficient
w = [(1,1)]

def norm(p):
    (n,c) = p.pop()
    while p:
        (m,d) = p.pop()
        if m == n: # collect up terms ex: w + w = 2w
            c += d
        elif m > n: # increase the power
            res.append((n,c))
            n = m
        elif m < n: # eat the term
            pass
    res.append((n,c))
    return res



def add(p,q):
    return norm(p + q)
def add(*ps):
    n,c = 0,0
    for p in reversed(ps):
        for (m,d) in reversed(p):
            if m == n:
                c += d
            elif m < n:
                pass
            elif m > n:
                res.append((n,c))
                n,c = m,d
    return reversed(res)

def mono_mul((n,c), p):
    

# mul is left distributive
def mul(p,q):

We sometimes complain that the definition of addition in coq on Nats is assymettric, requiring commutativity to be a theorem. But addition on ordinals really is assymmettric

(* a intrinsically symmettric definition of nat addition. Weird induction pattern though? *)
let add a b = match a,b with
        | Succ a, Succ b => Succ Succ (add a b)
        | Zero, b = b
        | a, Zero = a

ground truth of ordinal arithmetic is diagrams https://jdh.hamkins.org/counting-to-infinity-poster/

instrinsically sorted lists. Intertwine type slist = Succ of slist | Accept of slist | Nil type slist = {start : int, diffs : list nat}

“brower” ordinals

Ord :=
Z : Ord
| Suc : Ord -> Ord
| Lim : (nat -> Ord) -> Ord

https://drops.dagstuhl.de/storage/00lipics/lipics-vol084-fscd2017/LIPIcs.FSCD.2017.11/LIPIcs.FSCD.2017.11.pdf Nested Multisets, Hereditary Multisets, and Syntactic Ordinals in Isabelle/HOL

acl2 ordinals https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=abb015371fe03e28fbbf4f30d0658177183c0a09 Ordinal Arithmetic in ACL2. I see, yes they are using a multiset representation. Basically ordered mutisets using repetition. The more efficiennt thing the count multiset

https://arxiv.org/pdf/2208.03844 TYPE-THEORETIC APPROACHES TO ORDINALS

https://scholar.google.se/citations?view_op=view_citation&hl=en&user=-0ALlRsAAAAJ&citation_for_view=-0ALlRsAAAAJ:_kc_bZDykSQC Set-theoretic and type-theoretic ordinals coincide

https://www.cs.bham.ac.uk/~mhe/TypeTopology/Ordinals.CumulativeHierarchy.html adga ordinals

https://www.cs.bham.ac.uk/~mhe/TypeTopology/Ordinals.CumulativeHierarchy.html

https://arxiv.org/abs/1610.08027 multisets in type thoery

https://projecteuclid.org/journals/notre-dame-journal-of-formal-logic/volume-30/issue-1/Multiset-theory/10.1305/ndjfl/1093634995.pdf multiset theory Aczel

Is there a way to dynamically count your iterations using an ordinal notation?

Both add and mul are associative

https://en.wikipedia.org/wiki/Admissible_ordinal Kripke platek set theory

Graham mentioned HOD. https://en.wikipedia.org/wiki/Ordinal_definable_set hereditarily ordinal definable. Combine the hereditary finite serts with an ordinal notation? V omega. Presumably the hereditary finite sets are capped by something akin to omega? Use Paulson’s enumeration function?

Operations on orders / ordered sets:

  • sum = concat the orders. Hasses diagram of b is plugged on top of a.
  • multi. lex prod. Little copy of every hasse of b at every vertex of a
  • exp - monotonic functions?

ordinal exponentation https://math.stackexchange.com/questions/278992/how-to-think-about-ordinal-exponentiation

surprising. Why isn’t it monotonic functions. a^b is finite (partial) maps from b to a. This can be represented as a sorted list of tuples. [(a,b)] Basically comparing these lists lexwise will find the largest disagreement and compare there.

An extension to multisets is rather than a -> Nat do a -> Ord

This is probably obvious from the category perspective. The sum , product and epxonent of regualr sets is disjoint sum, cartesian product, and function space. This is just a natrual way to add orders to that

eps_0 obeys w^eps_0 = eps^0 . https://en.wikipedia.org/wiki/Epsilon_number. This is starting to feel like the kind of thing scott was doing with models of the lambda calculus

nat induction is in some sense transfinite induction up to w? So regular for nat induction is bounded induction in this sense.

https://hackage.haskell.org/package/Ordinals-0.0.0.2/docs/src/Math-Ordinals-MultiSet.html#Ordinal

# https://hackage.haskell.org/package/Ordinals-0.0.0.2/docs/src/Math-Ordinals-MultiSet.html#Ordinal
import itertools
def multiset(xs):
    return tuple(sorted(xs))

zero = ()
def from_int(n):
    return tuple(itertools.repeat(zero, n))

from enum import Enum
class Comparison(Enum):
    LT = -1
    EQ = 0
    GT = 1
def compare(xs,ys):
    if xs == zero and ys == zero:
        return 0
    elif xs == zero:
        return -1
    elif ys == zero:
        return 1
    else:
        c = compare(xs[0], ys[0])
        if c == 0:
            return compare(xs[1:], ys[1:])
        else:
            return c

def add(xs, ys):
    if ys == zero:
        return xs
    else:
        return tuple(itertools.takewhile(lambda x: compare(x, ys[0]) >= 0, xs)) + ys

one = from_int(1)
two = from_int(2)
three = from_int(3)
assert from_int(0) == zero
add(three,three)
assert add(three,zero) == three
assert add(zero,three) == three
assert add(zero,zero) == zero
assert add(two,three) == from_int(5)

def omega(n):
    return (n,)
w = omega(from_int(1))

assert add(omega(zero) , omega(zero)) == two
assert add(omega(zero), two) == three
assert add(one, w) == w
assert add(w, one) != w
#add(two, omega(zero))
add(w, one)
add(w,w)


def is_limit(xs):
    return len(xs) != 0 and xs[-1] != zero
assert not is_limit(zero)
assert not is_limit(one)
assert is_limit(w)
assert not is_limit(add(w,one))

omega(w)



((((),),),)

() < ((),) # stock lex ordering just works?

True

# no not a valid concept. pred_lim(w^2) =? w*n ???
def pred_lim(xs):
    return xs[:-1] + pred_lim(xs[-1])


def succ_lim(xs):


# No this is impossible. We have to recur into xs even though the limit definition is recusrive on ys.
def add1(xs,ys):
    if ys == zero:
        return xs
    elif not is_limit(ys): # zero at end
        return add1(xs, ys[:-1]) + ((),)
    elif xs < ys[-1]:
        return ys
    else:
        return add1(xs, ys[:-1])

assert add1(zero, zero) == zero
assert add1(zero, one) == one
assert add1(one, zero) == one
assert add1(one, one) == from_int(2)
assert add1(one, two) == from_int(3)
assert add1(two, one) == from_int(3)
assert add1(two, two) == from_int(4)
print(add1(one,w))
print(add(one, w))
print(add(w, three))
assert add1(one, w) == w
assert add1(w, one) == add(w, one)





def mul(xs, ys):
    if xs == zero:
        return zero
    else:


def msum(xs, ys):
    return multiset(xs + ys)

def mdiff(xs, ys):
    t = list(xs)
    for y in ys:
        try:
            t.remove(y)
        except ValueError:
            pass
    return multiset(t)



A = [1,2,3,4,1]
A.remove(1)
A.remove(1)
A.remove(1)
A

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

Cell In[32], line 4
      2 A.remove(1)
      3 A.remove(1)
----> 4 A.remove(1)
      5 A


ValueError: list.remove(x): x not in list

# just a + bw + cw^2 + ... is a reasonable subset to handle
# use lex ordering 
from enum import Enum
Order = Enum('Order', 'LT GT EQ NGE NLE')
def compare(a,b):
    if len(a) < len(b):
        return Order.LT
    elif len(a) > len(b):
        return Order.GT
    else:
        if a == b:
            Order.EQ
        if a < b:
            return Order.LT
        if a > b:
            return Order.GT
        
    
compare((0,2), (0,3))


def add(x,y):
    if len(x) < len(y):
        return y
    else:
        y = (0,) * (len(x) - len(y)) + y 
        return tuple([x[i] + y[i] for i in range(len(x))])

o = (1,0)
add(o,(4,))

def mul(x,y):
    # trim zeros
    # convolve return x + y
    # multiplicais is right ristribution a*(b + c) = a*b + a*c
    # https://en.wikipedia.org/wiki/Ordinal_arithmetic
    pass




/tmp/ipykernel_9122/1569711812.py:17: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  add_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:17: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w + 1' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  add_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:17: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w + 2' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  add_df.at[a, b] = result
0 1 2 w w + 1 w*2 w**2
0 0.0 1.0 2.0 w w + 1 w*2 w**2
1 1.0 2.0 3.0 w w + 1 w*2 w**2
2 2.0 3.0 4.0 w w + 1 w*2 w**2
w w w + 1 w + 2 w*2 w*2 + 1 w*3 w**2
w + 1 w + 1 w + 2 w + 3 w*2 w*2 + 1 w*3 w**2
w*2 w*2 w*2 + 1 w*2 + 2 w*3 w*3 + 1 w*4 w**2
w**2 w**2 w**2 + 1 w**2 + 2 w**2 + w w**2 + w + 1 w**2 + w*2 w**2*2 
/tmp/ipykernel_9122/1569711812.py:22: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  mul_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:22: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w + 1' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  mul_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:22: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w*2' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  mul_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:22: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w**2' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  mul_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:22: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  mul_df.at[a, b] = result
/tmp/ipykernel_9122/1569711812.py:22: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'w*2' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  mul_df.at[a, b] = result
0 1 2 w w + 1 w*2 w**2
0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1 0.0 1.0 2.0 w w + 1 w*2 w**2
2 0.0 2.0 4.0 w w + 2 w*2 w**2
w 0.0 w w*2 w**2 w**2 + w w**2*2 w**3
w + 1 0.0 w + 1 w*2 + 1 w**2 w**2 + w + 1 w**2*2 w**3
w*2 0.0 w*2 w*4 w**2 w**2 + w*2 w**2*2 w**3
w**2 0.0 w**2 w**2*2 w**3 w**3 + w**2 w**3*2 w**4 
# polynomial as power of n with number [(n,a)]
# addition and multiplication are associative
# pick convetion of left assocated or right associated?
"""
def trim(p):
    return [(c,n) for c,n in p if c > 0]

def add_mono(x,y):
    [(c1,n1)] = x
    [(c1,n2)] = y
"""




def right_assoc(t, tail=None):
    match t:
        case ("*", a ,b):
          return right_assoc(a, right_assoc(b, tail))
        case _:
            if tail==None:
                return t
            else:
                return ("*", t, tail)

def add




# actually the acl2 paper seemsl ike it has this laid out
from z3 import *
Ord = DeclareSort('Ord')
wz3 = Const('w', Ord)

n,m = Consts('n m', Nat)
#https://theory.stanford.edu/~nikolaj/programmingz3.html#sec-special-relations
le = TotalOrder(Ord,0)
inj = Function('inj', Ord, Nat)
ForAll([n,m], (n == m) == (inj(n) == inj(m)))

ForAll([n], le(inj(n), w)) # w is greater than all integers

# w is less than or equal to anything greater than intgeers. It is the least upper bound of the integers.
Implies(ForAll([n], le(inj(n),a)), le(w, a))

sup = Function(*"sup", Set(Ord), Ord)
sup_def = ForAll([X], Implies(ForAll([a], Implies(X[a], le(a, sup(X)))), s

succ = Function("succ", Ord, Ord)
ForAll([n], And(n != succ(n), le(n,succ(n))))
ForAll([n,m], le(n, m) == Or( m == succ(n), le(succ(n), m)))
ForAll([n,m], le(n,m) == le(succ(n),succ(m)))
ForAll([n], le(n, succ(n))) # but also it's the only strictly equal

ForAll([n], inj(Nat.succ(n)) == succ(inj(n)))

add = Function("add", Ord, Ord,Ord)

ForAll([n,m], add(n,succ(m)) == succ(add(n,m)))


is_lim = Function("is_lim", Ord, B)
is_lim_def = ForAll([x], is_lim(x) == Not(Exists([r], x == succ(r))))

is_lim 

# That one stack exhange on first order theory of ordinals.
plus = Funciton
plus_def = ForAll([n,m], plus(n,m) == If(m == 0, n, 
                                      If(is_succ(m), plus(n,pred(m)),
                                      If(is_lim(m), le(b,m) plus(n,b))))
is_lim(m) => forall le(plus(n,m),b) 


# Because we have that magic total order (magic? No it isn't magic)

Ord = Datatype("Ord")
Ord.declare("cons", ("car", ), ("n", Ord))
Ord.declare()

from transfinite import w

1 + w
(w*w + 1) + (w + 1)
#(w*w + 1) + (w + 1) + (w*w + 1)
((((w*w + 1) + 1) + w)) + 1
(w*w*w + 4) + (w*w*w + 1)

(w + 1) * (w + 4)

print(hash(w + 4))
hash(w + 4)


-1926672114936953222





-1926672114936953222

# iterated multisets. Hereditary multisets. multiset theory
emp = []
def nat(n):
    if n == 0:
        return emp
    return [(emp, n)]

# use multiset ordering

# a lex (m, q) 
[(nat(1), m), (nat(0), q)]
# lex (p,0,r)
[(nat(2), p), (nat(0), r)]

# you can't define prev((1,0,0)). It's a limit ordinal. not exists r, q = succ(r)

Cardinals

cardinals inaccessible https://en.wikipedia.org/wiki/Large_cardinal https://en.wikipedia.org/wiki/Supercompact_cardinal https://en.wikipedia.org/wiki/Woodin_cardinal

https://en.wikipedia.org/wiki/The_Higher_Infinite

https://en.wikipedia.org/wiki/Scott%27s_trick

https://en.wikipedia.org/wiki/Aleph_number

https://en.wikipedia.org/wiki/Beth_number

https://en.wikipedia.org/wiki/Continuum_hypothesis

Multiset orderings

If I sttore the multiset in either `list (e, multiplicity) or sorted repeated list form. Doesn’t lex ordering do the right thing? First it checks that the multiplicitlies of the higher stuff. Which ever thing I remove, I can put more stuff deeper in the lex ordering. The multiplicity thing works with too. (w, 10) > (w,9)

https://en.wikipedia.org/wiki/Dershowitz%E2%80%93Manna_ordering

Expansion and search trees.

Order summation. Disjoint sum of underling sets and the sayeverything in Right is greater than everything in Left. This shows the composition of two prcoesses is terminating.

Lexiocgraphic product. Tuple of underlying sets. Nesting of two terminating properties is terminating. How do I square that this feels like two nested for loops with lex being part of ackermann termination also?

Multiset ordering allows deletions from the set.

Delete one and add any number of things less than the deletion. A sequence of these. Note that this makes the size of the thing explode.

Proof mining of termination proofs may give complexity bounds

A well ordered search process is termnating because you expand the start node into it’s lesser children.

A multiset order over an empty

Proof multiset ordering is terminating. Konig’s lemma. Assume the multiset expansion tree (the multiset order tree) is infinite, then we find a path that is infinite. But this path is an infinite chain in the unbderlying order which was assumed terminating. Contradiction.

Monomials x^2 y^3 z^1. Commutativty of mulitplication makes monomials like multisets. Guarentees termination of buchberger or multivariate division.

Multisets can be represents as xxyyyz or [2,0,3,0,0,0,1,0 …] This is an infinite sequence of onlyu finitely many nonzeros. This is reasonable thing to think of as the “limit” are arbitrarily large lexicographic orders This is w^w

Ordinals are total/linear well founded orders. A stronger requirement but related

Hydra game epsilon0

https://lawrencecpaulson.github.io/2022/10/26/Multiset-Ordering.html e art of coimputer programming vol 1. pp382

multiste of order with order type a w^a

So consider the order 0 -> 1 -> 2. What is it’s multiset order? {0: n, 1:m, 2:k} which is a lex order of (k,m,n) where k,m,n are nats.

https://dl.acm.org/doi/10.1145/359138.359142 Proving termination with multiset orderings. Dershowitz and Manna

def succ(x):
    if isinstance(x, int):
        return x + 1
    else:
        

def sup(x):

def add(x,y):
    match x:
        case 0:
            return y
        case int(n):


# Here I'm showing how toi enumerate the orderings if they are finitary

# disjoint sum of two terminating relations is terminating
def disjoint_sum(P,Q):
    return [((0,a), (0,b)) for (a,b) in P ] + [((1,a), (1,b)) for (a,b) in Q ]
# we can also totalize it. by adding in all the things that put the lower one lower.
def total_disjoint_sum(P,Q):
    PS = [x for p in P for x in P]
    QS = [x for q in Q for x in Q]
    return [((0,a), (0,b)) for (a,b) in P ] + [((1,a), (1,b)) for (a,b) in Q ] + [((0,a), (1,b)) for a in PS for b in QS]

def lex_prod(P,Q):
    return [((a1,b1),(a2,b2)) for (a1,b1) in P for (a2,b2) in Q if a1 <= a2 and b1 <= b2]

def multiset(P,Q):






from enum import Enum
Order = Enum('Order', ['GR', 'EQ', 'NGE']) # >, =, !>=
default_ord = lambda a,b: Order.EQ if a == b else Order.GR if a > b else Order.NGE 
def lex(a,b, ord=default_ord):
    for a,b in zip(a,b):
        match ord(a,b):
            case Order.GR:
                return Order.GR
            case Order.EQ:
                continue
            case Order.NGE:
                return Order.NGE
    return Order.EQ


lex([2,2], [2,1])



<Order.GR: 1>

from collections import Counter
def diff(xs, ys, order=default_ord):
    while len(ys) != 0:
        y = ys.pop()
        xs.remove(y)




def mul(ms,ns,ord=default_ord):
    nms = diff(ns,ms,ord)
    mns = diff(ms,ns,ord)
    if len(mns) == 0 and len(mns) == 0:
        return Order.EQ
    elif all(any(ord(m,n) == Order.GR for m in mns) for n in nms):
        return Order.GR
    else:
        return Order.NGE
    


# a different rep is P : A -> A -> Bool
def disjoint_sum(P,Q):
    def res((taga,a), (tagb,b)):
        if taga < tagb
            return "GT"
        elif taga > tagb:
            return "LT"
        elif taga == 0 and tagb == 0:
            return P(a,b) 
        elif taga == 1 and tagb == 1:
            return Q(a,b)
        
    return lambda : iP(a1,a2) or Q(a1,a2)

from z3 import *
B = BoolSort()
S = DeclareSort('S')
Rel = ArraySort(S,S,B)
P,Q,R = Consts('P Q R', Rel)


trans = Function("trans", Rel, B)
trans_close = And(trans(R), ForAll([P], Implies(trans(P), sebeq(R,P)))) 

total
wellfounded = Function("wellfounded", Rel, B)


homomap(F) = Implies(R(a,b), P(F(a), F(b)))

ordertype(P,a) = Exists([F], homomap(F,P,a))

def wellfounded_induction(R, P):
    return Implies(And(wellfounded(R), ForAll([x], Implies(ForAll([y], Implies(R[y,x], P(y))), P(y)))),
                #--------------------------------------------------
                                        ForAll([x], P(x)))

Ord = DeclareSort("Ord")
le = TotalOrder(Ord,0)


zero = Const('zero', Ord)
succ = Function('succ', Ord, Ord)

succ_def = ForAll([x], le(x, succ(x)))
lim = Function("lim", ArraySort(Nat, Ord), Ord) #????

Ordinals

Ordinals notations https://en.wikipedia.org/wiki/Ordinal_notation are lik systemaic ways of labelling ordinals. They don’t described every posible ordinal.

Ordinals are a generalizatin of numbrs

Countable ordinals. 1 …. omega is countabe. 0 -> omega, 1 -> 0, 2 -> 1 … is an enemeration. It isn’t an order repsecting enumeration though. So “infinite” numbers can be finitely represented. type omega_plus_1 = Omega | Fin of nat. We are used to this from floats for example So polynomials of omega is maybe a first place to state. Those are implementable as typical lists of coefficients. They have funky addition and mult properties (funky mult happens in matrices and quaternions, but noncommutative addition is more unusual). But then ordinals typically allow going up to new stuff (exponentiation and beyond).

https://www.khoury.northeastern.edu/home/pete/pub/cade-algorithms-ordinal-arithmetic.pdf algorithms for ordinal arithemtic. ACL2

https://link.springer.com/chapter/10.1007/BFb0023868 Ordinal arithmetic with list structures dershowitz reingold

Termination as mapping into ordinals. Measure is the map. Simple ones into integers. Lexicographic and w^n

https://mathoverflow.net/questions/456649/lists-as-a-foundation-of-mathematics lists as foundation of mathematics.

https://dl.acm.org/doi/10.1145/3372885.3373835 Three equivalent ordinal notation systems in cubical Agda https://www-sop.inria.fr/marelle/gaia/RR8407.pdf Implementation of three types of ordinals in Coq https://www-sop.inria.fr/marelle/gaia/

(* cons(a,n,b) = w^a(n + 1) + b  *)
Inductive T1 : Set :=
zero : T1
| cons : T1 -> nat -> T1 -> T1

https://github.com/sympy/sympy/issues/8668 sympy issue on ordinal arithmetic https://github.com/sympy/sympy/blob/master/sympy/sets/ordinals.py

from sympy.sets.ordinals import *
w = omega
z = ord0
print(3 + w + 2 * w)
print(2 * w)

https://github.com/ajcr/transfinite pip instal transfinite python package

# https://github.com/ajcr/transfinite/blob/master/notebooks/ordinal_arithmetic_basics.ipynb notebook
from transfinite import w, factors
print(w*w + 1)
print(1 + w)
print(dir(w)) # addend', 'coefficient', 'exponent', 'is_delta', 'is_gamma', 'is_limit', 'is_prime', 'is_successor'
print(w.is_limit()) # true
print(w.is_delta()) # mutliplicatively indecomposable
print((w + 1).is_limit()) #false
print(w ** w)
print( w <= w)
print(repr(w))
fs = factors(w*w) 
print(dir(fs)) # as_latex', 'factors', 'ordinals', 'product'

# based in cantor normal form https://github.com/ajcr/transfinite/blob/master/transfinite/ordinal.py
#          (exponent)
#         ^
#        w . (copies) + (addend)

Prime ordinals and facotring

https://web.mit.edu/dmytro/www/other/OrdinalArithmetic.py https://web.mit.edu/dmytro/www/other/OrdinalNotation.htm

https://www.jstor.org/stable/20118717 rathjen 2006 Theories and Ordinals in Proof theory Rathjen the art of ordinal analysis https://www1.maths.leeds.ac.uk/~rathjen/ICMend.pdf

https://github.com/coq-community/hydra-battles https://coq-community.org/hydra-battles/doc/hydras.pdf book chapter 3 is on ordinals in coq

https://en.wikipedia.org/wiki/Goodstein%27s_theorem - hydra games. unprovable in peano arith

https://math.andrej.com/2008/02/02/the-hydra-game/ kirby and paris Accessible Independence Results for Peano Arithmetic

http://www.madore.org/~david/math/hydra.xhtml javascript of the game

hydra is kinda remniscent of hackenbush

https://www.youtube.com/watch?v=uWwUpEY4c8o&ab_channel=PBSInfiniteSeries PBS infinite series on hydra game

https://en.wikipedia.org/wiki/Bachmann%E2%80%93Howard_ordinal large countable ordinal

https://en.wikipedia.org/wiki/Kripke%E2%80%93Platek_set_theory weak set theory. preciative part. Separation only works on delta_0 bounded formula. I like that

https://en.wikipedia.org/wiki/Constructive_set_theory wow this a a whole rabbit hole

https://ncatlab.org/nlab/files/AczelRathjenCST.pdf notes on constructive set theory - rathjen aczel

Γ₀

https://en.wikipedia.org/wiki/Puiseux_series mentined that stuff generalzes this. A power series with fractional powers.

https://en.wikipedia.org/wiki/Hahn_series a notion of series with domain that is well ordered?

https://en.wikipedia.org/wiki/Levi-Civita_field contains infintesimal and infinite stuff

https://en.wikipedia.org/wiki/Epsilon_number fixed points of exponential maps

import math
class Rational():
  def __init__(self, numb, den):
    gcd = math.gcd(num,den)
    self.num = num / gcd
    self.den = den / gcd
  def __add__(self, other):
    return Rational(self.num * other.den + other.num * self.den, self.den * other.den)
  def __mul__(self, other):
    return Rational(self.num * other.num, self.den * other.den)
  def __sub__(self, other):
    return Rational(self.num * other.den - other.num * self.den, self.den * other.den)
  def __truediv__(self, other):
    return Rational(self.num * other.den, self.den * other.num)
  def __repr__(self):
    return f"{self.num}/{self.den}"
  def __eq__(self, other):
    # or self.num * other.den == other.num * self.den
    return self.num == other.num and self.den == other.den
  def __lt__(self, other):
    return self.num * other.den < other.num * self.den

def Complex():
    def __init_(self, real, imag):
        self.real = real
        self.imag = imag
    def __add__(self, other):
        return Complex(self.real + other.real, self.imag + other.imag)

def BigNum():
  self __init__(self,n):
    self.digits = []
    while n > 0:
      self.digits.append(n % 10)
      n = n // 10
    def value(self):
      return sum([d * 10 ** i for i, d in enumerate(self.digits)])
  def __add__(self, other):
    # cheating: return BigNum(self.value() + other.value())
    res = []
    carry = 0
    for i in range(max(len(self.digits), len(other.digits))):
      s = self.digits[i] if i < len(self.digits) else 0
      o = other.digits[i] if i < len(other.digits) else 0
      res.append((s + o + carry) % 10)
      carry = (s + o + carry) // 10
  #def __mul__(self,other):
  #  res = BigNum(0)
  #  for i in range(len(self.digits)):
  #    for j in range(len(other.digits)):
  #     res += BigNum(self.digits[i] * other.digits[j]) * BigNum(10 ** (i + j))
  #  return res

class Quaternion():
  def __init__(self, c,i,j,k):
    self.c = c
    self.i = i
    self.j = j
    self.k = k
  def __add__(self, other):
    return Quaternion(self.c + other.c, self.i + other.i, self.j + other.j, self.k + other.k)
  def __mul__(self, other):
    return Quaternion(self.c * other.c - self.i * other.i - self.j * other.j - self.k * other.k,
                      self.c * other.i + self.i * other.c + self.j * other.k - self.k * other.j,
                      self.c * other.j - self.i * other.k + self.j * other.c + self.k * other.i,
                      self.c * other.k + self.i * other.j - self.j * other.i + self.k * other.c)

# https://en.wikipedia.org/wiki/Continued_fraction
# Another way of representing fractions that has nice properties.
def ContFrac():
  # this is the euclidean algorithm
  def __init__(self, num,den):
    self.coeff = []
    while num != 0:
      self.coeff.append(num // den)
      num, den = den, num % den

def golden_ratio(): # an irratinal number with infinite expansion 
  while True:
    return 1


# using built in complex and fraction
from fractions import Fraction
print(Fraction(1,10) )
print(1 + 1.j)



# another method, embedding into matrices
import numpy
def complex(r,i):
  return np.array([[r,-i],[i,r]])

https://docs.python.org/3/library/numbers.html#module-numbers abstract based classes for numbers

Large Numbers

name the smallest numnber.

tree(3) https://www.youtube.com/watch?v=3P6DWAwwViU&ab_channel=Numberphile graham’s number