Treeifying Graphs: Tree Decomposition
Trees are good. For many questions you can process them from leaves to parents. If you remove a vertex, it will cut the tree apart. Communication can only happen through a single path.
There are quite a number of decompositions of graphs. The very word decomposition suggests that you are probably breaking the graph apart into simpler pieces. Maybe this breaking apart in in some sense recursive or inductive leading to a divide and conquer approach to dealing with the graph. Many of these decompositions are about describing a method to construct the graph by combining simpler pieces.
- https://en.wikipedia.org/wiki/Tree_decomposition
- https://en.wikipedia.org/wiki/Pathwidth
- https://en.wikipedia.org/wiki/Modular_decomposition
- https://en.wikipedia.org/wiki/Branch-decomposition
- https://en.wikipedia.org/wiki/Graph_partition
A blog post I want to write but can’t figure out how to is on the general phenomenon of trying to “treeify graphs”. This is the game we seem to play trying to model graphical topics in egraphs, which only comfortably handle pure trees. An intuition I’ve been following is whether there is a way to bake in something like a dynamic tree decomposition into an egraph data structure. I don’t have anything concrete though. So this is a smattering of etudes and thoughts.
Tree decompositions are one example of this treeifying graph phenomenon. But there are others
- Regular expressions and DFAs. Regular expressions are trees. Automata are graphy (although with an odd notion of homomorphism or equality. Often only observable behavior is relevant). They are interconvertible, but regexes may be treatable in simple compositional ways See Tarjan paper https://dl.acm.org/doi/10.5555/892083 Solving path problems on directed graphs. You can treat DFA problems equationally by axiomatizing kleene algerba. https://www.philipzucker.com/bryzzowski_kat/ https://github.com/mgree/katbury Not typically considered the best approach.
- Structured languages and CFGs. Relooper turns cfgs into structured control flow which are syntax trees. MLIR and RVSDG try to make the control flow graph even more structured and tree like in some respects. Having
ifandwhilesyntax trees makes doing weakest precondition analysis much easier for example. You can do some equational term-like rewriting onwhileloops andifalso for loop fusion and things. - Algebraic Graphs. Mokhov, Schrijver, Kidney. Not that dissimilar from the graph theorists notion of decomposition. A focus on the algebraic laws of the construction operators (semiring).
- Tree Decomposition. Metis. Domain Decomposition. Largely what I’mm talk about today
- String diagrams and categorical combinators. This is perhaps related to Series parallel decomposition as monoidal categories have a horizontal (parallel) and vertical composition (series). This particular trick is kind of what brought me into egraphs https://www.philipzucker.com/rust-category/
- Algebra of Programming. Backhouse.
- Lambda term technology. De bruijn indices, named reprs. Names are the analog of vertex labels in graphs, a kludge. Lambdas muddy the water about whether they are really “terms” because the variables make them more entangled than a nice simple tree. You can embed lambdas as graphs by having variables backedge point to their binding sites and lambda normalization as graph rewriting. Optimal reduction https://dl.acm.org/doi/10.1145/96709.96711 has some nice diagrams like this.
Different communities have very different perspectives here. The graph theory / Theory of computation people seem to prefer the tree decomposition style stuff of often undirected unrooted graphs where vertices do not have ports/ordered children. Programming language people seems to prefer things that are more AST like, with roots and ported vertices / ordered children. I would like to understand how these perspectives could be fused or played off each other.
Graphs come in a number of flavors. The word graph does not mean one thing. It is dependent on the community you are talking to
- multigraphs can have more than one edge between the same two nodes
- labels on the edges and/or vertices or not
- Labelled and/or ordered ports on the vertices or not. Input vs output ports.
- Single output port or many.
- DAG, tree, or graph.
- Rooted or not.
- Directed vs undirected
I dunno. If you’ve got something to say, DM me or email me. It’s an interesting set of topics.
Tree Decomposition
The tree decomposition is in particular interesting because it gives a knob of sorts to dial between trees and more general graphs. A good tree decomposition can be useful to solve certain graph problems fast via dynamic programming and tree decomposition has some relationship to good elimination orderings (elimination being a process to fuse together vertices one by one).
First let’s look at a simple tree decomposition of a path graph.
import networkx as nx
def mydraw(G):
pos = nx.nx_agraph.graphviz_layout(G, prog="dot") # Requires pygraphviz
nx.draw(G, pos, with_labels=True)
G = nx.path_graph(5)
mydraw(G)
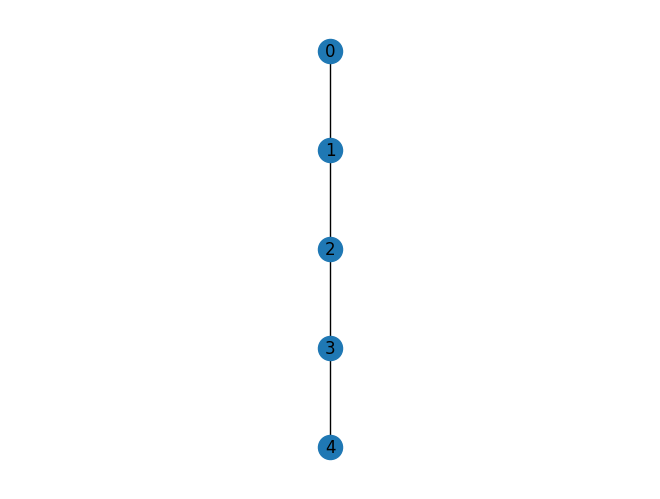
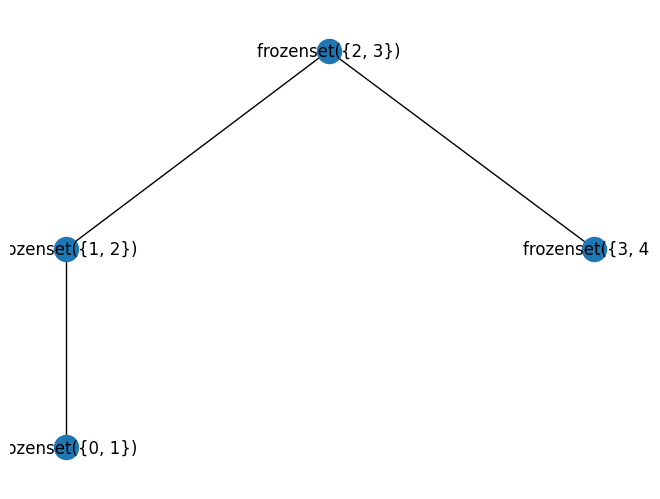
The function treewidth_min_degree is a heuristic algorithm to find a decent tree decomposition. The number quoted is not necesdsarily the actually treewdith (which is the size of the smallest bag - 1 of the tree decomposition with the smallest)
w, TD = nx.approximation.treewidth_min_degree(G)
print("treewidth", w)
mydraw(TD)
treewidth 1
A very untree-like graph is the complete graph
G = nx.complete_graph(5)
mydraw(G)
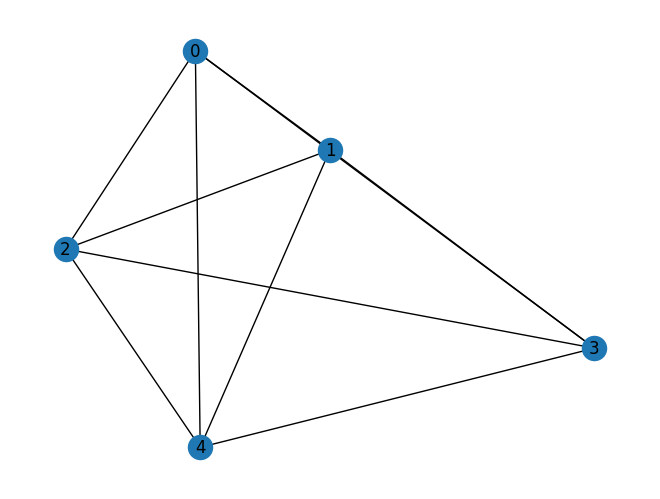
The tree decomposition can’t do anything with this, giving a tree decomposition with a single huge bag (always a valid answer according to the definition of tree decomposition, but not a useful one.)
w, TD = nx.approximation.treewidth_min_degree(G)
print("treewidth", w)
mydraw(TD)
treewidth 4

Another interesting graph is a loop
G = nx.cycle_graph(5)
mydraw(G)
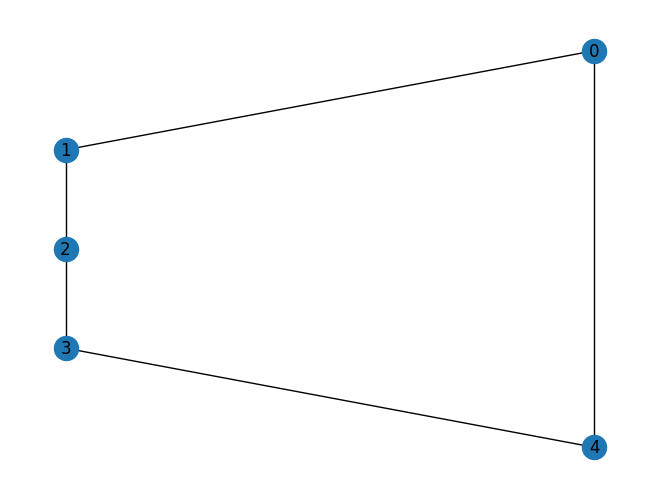
The tree decomposition here always has 4 in play. Note that the middle node of the decomposition has a 4 even though, 1 and 2 have no edge to 4.
The treewidth of 2 shows that a cycle is almost tree-like. It’s not so bad.
w, TD = nx.approximation.treewidth_min_degree(G)
print("treewidth", w)
mydraw(TD)
treewidth 2
Reifying Tree Decomposition into an AST
An interesting thing to do is actually reify this tree decomposition as a tree-like data structure for storing graphs.
Under the hood networkx graphs are neighbor dictionaries. But we could also represent graphs usefully as an adjacency list of tuples. This is yet another representation. It just has a hierarchical structure to the adjacency lists.
from dataclasses import dataclass
@dataclass
class TreeDecomp():
nodes: set[object]
edges : set[tuple[object, object]]
children : list["TreeDecomp"]
def to_graph(self):
G = nx.Graph()
def worker(td):
for i,j in td.edges:
G.add_edge(i,j)
for child in td.children:
worker(child)
worker(self)
return G
def tree_decomp(G) -> TreeDecomp:
w, G1 = nx.approximation.treewidth_min_degree(G)
center_nodes = nx.center(G1)
central_vertex = center_nodes[0]
seen = set()
def dfs(v):
seen.add(v)
children = [dfs(child) for child in G1.neighbors(v) if child not in seen]
return TreeDecomp(nodes=v, edges=set((i,j) for i in v for j in v if (i,j) in G.edges), children=children)
return dfs(central_vertex)
import pprint
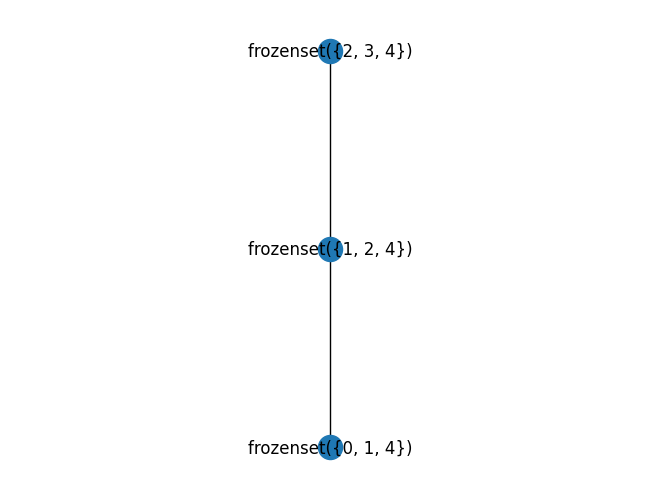
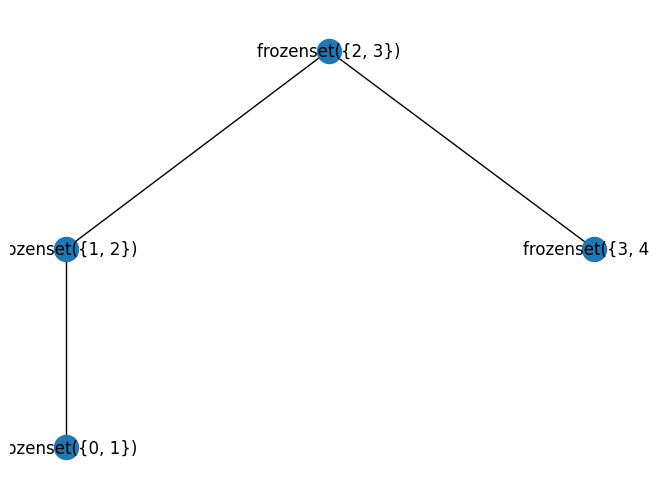
pprint.pprint(tree_decomp(nx.cycle_graph(5)))
mydraw(tree_decomp(nx.cycle_graph(5)).to_graph())
TreeDecomp(nodes=frozenset({1, 2, 4}),
edges={(1, 2), (2, 1)},
children=[TreeDecomp(nodes=frozenset({2, 3, 4}),
edges={(2, 3), (3, 2), (3, 4), (4, 3)},
children=[]),
TreeDecomp(nodes=frozenset({0, 1, 4}),
edges={(0, 1), (1, 0), (4, 0), (0, 4)},
children=[])])
Partitions
There is some similarity and interconnection between tree decompositions and graph partitioning.
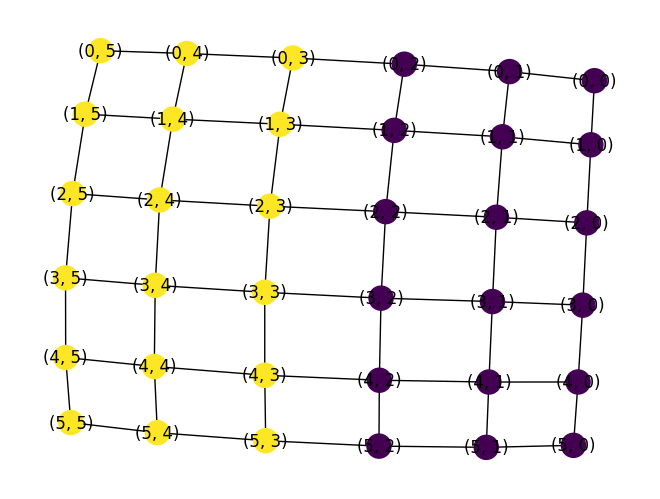
Graph partitioning software like METIS is used to break up meshes into smaller pieces and to derive a useful variable ordering to minimize fill in in linear algebra applications.
https://networkx.org/documentation/stable/reference/algorithms/community.html networkx also has a number of partitioning algorithms
import networkx as nx
import metis
G = nx.grid_2d_graph(6, 6)
(edgecuts, parts) = metis.part_graph(G, 2)
edgecuts
parts
nx.draw(G, node_color=parts, with_labels=True)
One can reify a recursive partition into a tree also.
This paper “Correspondence between Multilevel Graph Partitions and Tree Decompositions” claims that basically you can derive a tree decomposition from such a partition. It won’t necessarily be a good one. Here we can see that it has a bigger than necessary tree width.
from dataclasses import dataclass
@dataclass
class MultiLevel():
nodes : set[object] # nodes is implicit in the other data.
edges: set[tuple[object, object]]
subs: list["MultiLevel"]
def to_graph(self):
G = nx.Graph()
def worker(ml):
for i,j in ml.edges:
G.add_edge(i,j)
for sub in ml.subs:
worker(sub)
worker(self)
return G
def to_tree_decomp(self):
return TreeDecomp(nodes={v for ij in self.edges for v in ij}, edges=self.edges, children=[sub.to_tree_decomp() for sub in self.subs])
def multilevel(G):
if len(G) == 1:
return MultiLevel(nodes=set(G.nodes), edges=set(), subs=[])
else:
p1,p2 = nx.community.kernighan_lin_bisection(G)
G1 = G.subgraph(p1)
G2 = G.subgraph(p2)
edges = {(i,j) for i,j in G.edges if (i in p1 and j in p2) or (i in p2 and j in p1)}
return MultiLevel(nodes=set(G.nodes), edges=edges, subs=[multilevel(G1), multilevel(G2)])
import pprint
ml = multilevel(nx.cycle_graph(5))
pprint.pprint(ml)
MultiLevel(nodes={0, 1, 2, 3, 4},
edges={(2, 3), (0, 4)},
subs=[MultiLevel(nodes={3, 4},
edges={(3, 4)},
subs=[MultiLevel(nodes={3}, edges=set(), subs=[]),
MultiLevel(nodes={4}, edges=set(), subs=[])]),
MultiLevel(nodes={0, 1, 2},
edges={(1, 2)},
subs=[MultiLevel(nodes={2}, edges=set(), subs=[]),
MultiLevel(nodes={0, 1},
edges={(0, 1)},
subs=[MultiLevel(nodes={1},
edges=set(),
subs=[]),
MultiLevel(nodes={0},
edges=set(),
subs=[])])])])
pprint.pprint(ml.to_tree_decomp()) # This is a bad tree decomposition, but I think it is one. We could do a split and rebalnce move maybe to improve it.``
TreeDecomp(nodes={0, 2, 3, 4},
edges={(2, 3), (0, 4)},
children=[TreeDecomp(nodes={3, 4},
edges={(3, 4)},
children=[TreeDecomp(nodes=set(),
edges=set(),
children=[]),
TreeDecomp(nodes=set(),
edges=set(),
children=[])]),
TreeDecomp(nodes={1, 2},
edges={(1, 2)},
children=[TreeDecomp(nodes=set(),
edges=set(),
children=[]),
TreeDecomp(nodes={0, 1},
edges={(0, 1)},
children=[TreeDecomp(nodes=set(),
edges=set(),
children=[]),
TreeDecomp(nodes=set(),
edges=set(),
children=[])])])])
Questions: Kernighan lin seems like a great local jiggling method to improve a partitioning. Is there a translation of it to tree decompositions for local improvement?
Bits and Bobbles
Algebraic graphs doesn’t seem that different from the perspective of graph decompositions. They are a tree describing a way of constructing the graph out of operations. These operations may have nice algerbaic properties with respect to each other, like distributivity.
- https://www.cs.tufts.edu/comp/150FP/archive/andrey-mokhov/algebraic-graphs.pdf Algebraic Graphs with Class (Functional Pearl).
- https://arxiv.org/abs/2202.09230 United Monoids: Finding Simplicial Sets and Labelled Algebraic Graphs in Trees
- https://arxiv.org/abs/2403.02273 Let a Thousand Flowers Bloom: An Algebraic Representation for Edge Graphs
- https://dl.acm.org/doi/abs/10.1145/3704892 Formalising Graph Algorithms with Coinduction
- https://dl.acm.org/doi/10.1145/3473577 Algebras for weighted search
- https://dl.acm.org/doi/10.1145/2500365.2500613 Fun with semirings: a functional pearl on the abuse of linear algebra
I still find tree decomposition somewhat cloudy. I don’t think I would have defined the concept myself. I suspect it is defined in a way unnatural to my intended usage.
Trees are nice. You can often treat the leaves and then treat the parents of those leaves until you finish processing the whole graph. Many analyses or computations on trees are compositional in this sense. You can solve them by top down recursion, or single pass bottom up iteration.
Trees are also nice similarly because we can sometimes semantically interpret them compositionally (as a simple recursive functional program of type Tree -> Meaning ). Like the syntax tree add(one,two) is easy top interpret as the natural number 3 via a function eval : aexpr -> nat.
Graph rewriting is less straightforward (not impossibly so, but less) that term rewriting. It can be implemented mutationally, and it has a large body of theory, but still is a higher shelf to reach for than term rewriting.
Graphical structures come up very naturally when discussing lambdas a program representations. Alpha invariant names are often an indirection describing some kind of loopy connectivity.
For terms, we have a nice raft of data structures to work with. Algebraic datatypes, Hash conses and egraphs.
What I’ve begun to see as a general theme is that we try various scams to try and treeify graphs. I suspect a way forward is to bake some of these ideas into egraphs.
There is almost certainly not one graph decomposition to rule them all here. This feels similar to me to the idea of a view https://www.cs.tufts.edu/~nr/cs257/archive/phil-wadler/views.pdf in functional programming or in databases. Sometimes different tree-like views are useful.
It is also probably not possible or desirable to get unique or canonical or minimal decompositions. Heuristics can get you a very nice decomposition for cheap, but actually finding a best one is usually going to be NP-complete.
There are often local moves / equational reasoning for manipulating these treeified graphs. These local moves can greedily relax a suboptimal decomposition into a better one.
It is a curious phenomenon that low level languages like C and C++ make pointery graphs just as natural and easy as trees in some respects. The pure functional languages make this a harder thing to reach for. Rust makes this annoying via ownership. It is not insurmountable, you just need to build your own “address space” using an arena vector or map data structure. Still, this is one small step.
It is less straightforward to me the method to semantically interpret graphs. The graph probably needs to represent a system of constraints that needs to be solved in some way. We do have nice methods to semantically interpret lambda terms and some other things that are more graphy in nature. Non-wellfounded sets have nations like this (see vicious circles or aczel’s book)
Considering the edges as a relation edge(v1,v2), the relation is well founded for finite acyclic graphs. I would claim that well founded is just a mathematical rigorization of our intuitions of tree-like relations.
What graph theorists or networkx mean by trees is not really quite the same thing I (or compiler / PL people) mean by trees. The trees i like the best are AST-like or algebraic datatype like. They are rooted and have an ordering of the children of each node.
https://github.com/pa-ba/calc-graph-comp Beyond Trees: Calculating Graph-Based Compilers. This uses HOAS lambdas to model graphs. The opposite direction from what I was pointing out.
More on tree decompositions
https://types.pl/@sandmouth/112118720614314612 “a long time ago I tried to implement a unified isel + regalloc (+ representation selection between boxed/unboxed type, but that’s not a super common problem) for x86 based on a tree decomposition + dynamic programming. Worked decently well for simple loops, and let you solve directly in the domain w/o encoding to SAT/MIP. The representation selection ended up handling spills too…”
Tree decomposition is useful for dynamic programming combinatorial problems on graphs. The bag of vertices in the node is sort of the open interface. You can solve the subproblems parametrized on the values that the problem takes on at the interface.
Tree decompositions are also used in query optimization https://pages.cs.wisc.edu/~paris/cs784-s19/lectures/lecture5.pdf You can represent a databse query as a graph or hypergraph (hypergraphs are embeddable into graphs by making hyperedge nodes and turning the graph bipartite between hyperedge nodes and vertices).
Each hyperedge represents a relation and the vertices it connects to are the joining columns. You want to keep the working set small of intermeidate results. This corresponds to the bags in the hypertree deocmposition.
A databasee query is kind of a “proof relevant” form of counting solutions. We already know graph coloring is embeddable into a query if we put the complicated graph structure in thuery itself. https://www.philipzucker.com/sql_graph_csp/
The networkx algorithm performs elimination of veices (connecting neighbors when vertex is eliminated) and then uses that information to build a tree decomposition. https://networkx.org/documentation/stable/_modules/networkx/algorithms/approximation/treewidth.html#treewidth_min_degree
https://www.mdpi.com/1999-4893/12/9/198 Correspondence between Multilevel Graph Partitions and Tree Decompositions TH THe tree decomposition is like a sliding window moving over the graph where the window can’t have a vertex disappear asnd then reappear. The window has ast least one edge in it.
https://www.youtube.com/watch?v=gCZrasaG0vA
def treewidth(G):
vertices = list(G.nodes)
while vertices:
v.pop()
import itertools
def color(N, constr , td : TreeDecomp):
vs = list(td.nodes)
for coloring in itertools.product(range(N), repeat=len(vs)):
zip(vs,coloring)
for i,j in td.edges:
if constr(i,j):
if coloring[i] == coloring[j]:
break
pass
td.nodes
def ncolor(N, td : TreeDecomp):
subprobs = [ncolor(child) for child in td.children]
vs = list(td.nodes)
acc = {}
for coloring in itertools.product(range(N), repeat=len(vs)):
coloring = {i:c for i,c in zip(vs,coloring)}
if any(coloring[i] == coloring[j] for i,j in td.edges): # bad coloring
break
macc = 1
for subprob in subprobs:
pass
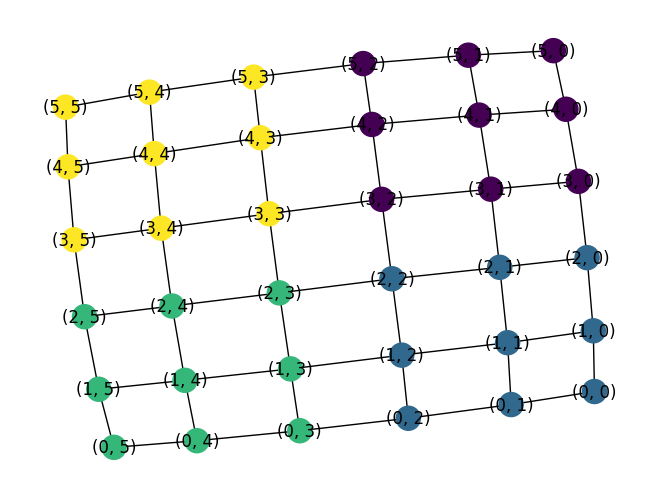
import networkx as nx
import metis
#G = metis.example_networkx()
G = nx.grid_2d_graph(6, 6)
(edgecuts, parts) = metis.part_graph(G, 4)
edgecuts
parts
nx.draw(G, node_color=parts, with_labels=True)
G = nx.cycle_graph(5)
nx.community.kernighan_lin_bisection(G)
({0, 1}, {2, 3, 4})
title: Treeifying Graphs date: 2025-02-03 —
Bits and Bobbles
Regular Expressions
String Diagrams and Series-Parallel Decomposition
https://en.wikipedia.org/wiki/Series%E2%80%93parallel_graph
class Series(NT):
s : object
t : object
import passagemath.graphs as graphs
G = Graph(Integer(2))
for i in range(Integer(3)):
G.add_clique([Integer(0), Integer(1), G.add_vertex(), G.add_vertex()])
tric = TriconnectivitySPQR(G)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[93], line 1
----> 1 import passagemath.graphs as graphs
2 G = Graph(Integer(2))
3 for i in range(Integer(3)):
ModuleNotFoundError: No module named 'passagemath'
Lambda Terms
Hash consings modulo alpha nominal techniques
from typing import NamedTuple
NT = NamedTuple
class Graph(NamedTuple):
def __add__(self, other):
pass
class Empty(Graph): pass
class Vertex(Graph): vert: object
class OverLay(Graph): g1: Graph; g2: Graph
class Conntect(Graph): g1: Graph; g2: Graph
def eval_graph(g : Graph) -> nx.Graph:
match g:
case Empty():
return nx.Graph()
case Vertex(vert):
return nx.Graph()
CFGs
Beyond Relooper: recursive translation of unstructured control flow to structured control flow (functional pearl) https://dl.acm.org/doi/10.1145/3547621 https://www.youtube.com/watch?v=qAeEWKr9wfU&ab_channel=ACMSIGPLAN Peterson Kasam Tokura https://toot.cat/@jamey/110399070056263970 https://dl.acm.org/doi/10.1145/2693261 Perfect Reconstructability of Control Flow from Demand Dependence Graphs
https://networkx.org/documentation/stable/reference/algorithms/dominance.html
from networkx.algorithms.dominance import immediate_dominators
a,b,c,d,e,f = "a b c d e f".split()
#G = nx.DiGraph([(1, 2), (2, 3), (3, 4), (3, 5), (4, 6), (5, 6)])
G = nx.DiGraph([(a, b), (b, c), (c, d), (c, e), (d, f), (e, f)])
nx.draw(G, with_labels=True)
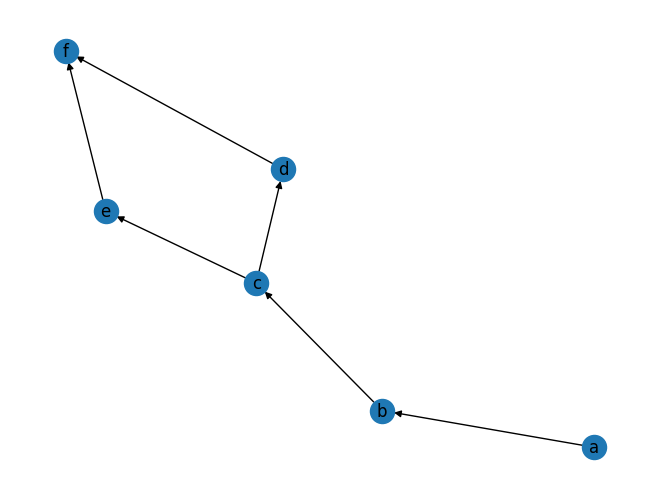
idom = immediate_dominators(G,a)
G1 = nx.DiGraph([(i,j) for j,i in idom.items()])
nx.draw(G1, with_labels=True)
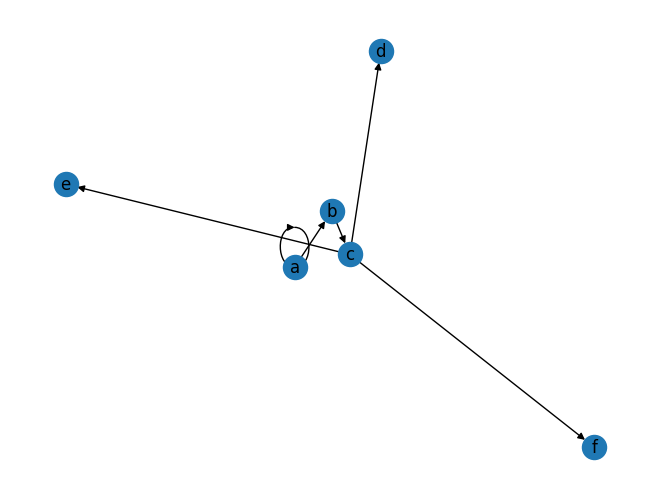
#nx.dfs_postorder_nodes(G, source=1)
def treeify(G):
seen = {}
backedge = []
def worker(i):
return (i, [worker(child) for child in G.neighbors(i) if child != i])
return worker(a)
treeify(G1)
('a', [('b', [('c', [('e', []), ('d', []), ('f', [])])])])
postorder = {v : i for i, v in enumerate(nx.dfs_postorder_nodes(G, source=a))}
def is_back(v1,v2):
if postorder[v1] > postorder[v2]:
return False
else:
return True
assert not is_back(a,b)
assert is_back(f,a)
def is_merge(v):
return len(list(G.predecessors(v))) > 1
is_merge(c)
False
def is_loop(v):
return any(is_back(v1,v) for v1 in G.predecessors(v))
assert all(not is_loop(v) for v in "abcdef")
class Break(NT): ind: int
class Block(NT): body: list[object]
class If(NT): cond: object; then: object; els: object
class Loop(NT): body: list[object]
def doTree(x):
(node, children) = x
if len(children) == 1:
Metis
Tree Decomposition
import networkx as nx
from networkx.algorithms.approximation import treewidth
G = nx.grid_2d_graph(4, 4)
nx.draw(G, with_labels=True)
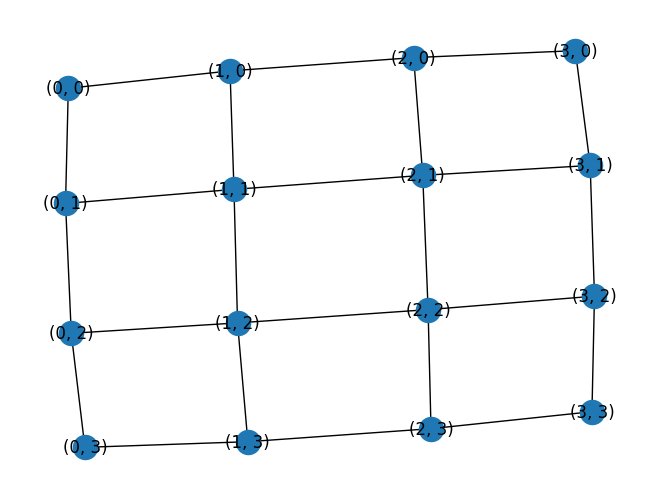
w, G1 = treewidth.treewidth_min_degree(G)
print("width", w)
nx.draw(G1, with_labels=True)
width 4
G = nx.path_graph(4)
#nx.draw(G, with_labels=True)
w, G1 = treewidth.treewidth_min_degree(G)
print("width", w)
nx.draw(G1, with_labels=True)
width 1
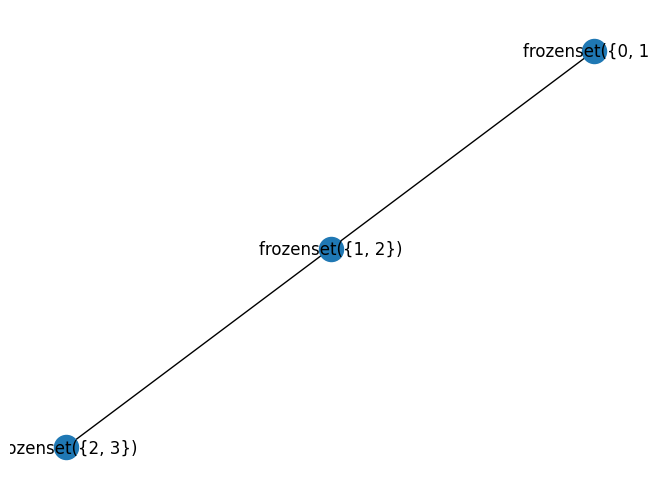
G = nx.cycle_graph(6)
#nx.draw(G, with_labels=True)
w, G1 = treewidth.treewidth_min_degree(G)
print("width", w)
nx.draw(G1, with_labels=True)
width 2
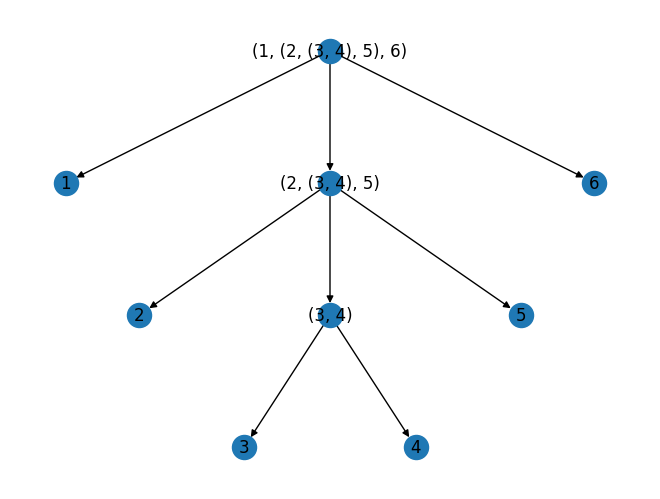
from typing import Iterable
def graph_of_tree(t):
def worker(t):
if isinstance(t, Iterable):
G.add_edges_from([(t, c) for c in t])
for c in t:
worker(c)
G = nx.DiGraph()
worker(t)
return G
G = graph_of_tree((1, (2, (3, 4), 5), 6))
pos = nx.nx_agraph.graphviz_layout(G, prog="dot") # Requires pygraphviz
#pos = nx.planar_layout(G)
nx.draw(G, pos, with_labels=True)
def draw_tree(G):
pos = nx.nx_agraph.graphviz_layout(G, prog="dot") # Requires pygraphviz
nx.draw(G, pos, with_labels=True)
from typing import NamedTuple
NT = NamedTuple
class Lam(NT): body: object
class App(NT): f: object; arg: object
class Var(NT): db: int
def graph_of_lam(t):
G = nx.DiGraph()
def worker(ctx, t):
if isinstance(t, Lam):
G.add_edge(ctx, t)
worker(t, t.body)
elif isinstance(t, App):
G.add_edge(ctx, t)
worker(t, t.f)
worker(t, t.arg)
elif isinstance(t, Var):
G.add_edge( ctx[t.db])
from dataclasses import dataclass
@dataclass
class TreeDecomp():
nodes: set[object]
edges : set[tuple[object, object]]
children : list["TreeDecomp"]
@classmethod
def empty():
return TreeDecomp(set(), set(), [])
@classmethod
def singleton(v):
return TreeDecomp({v}, set(), [])
@classmethod
def from_tree(t):
return TreeDecomp(t.nodes, t.edges, [TreeDecomp.from_tree(child) for child in t.children])
def add_vertex(self,v): #?
pass
def contains(self, v):
return v in self.nodes or any(child.contains(v) for child in self.children)
def add_edge(self,v1,v2):
"""
There is a distinction between adding an edge between already existing vertices and a new connecting vertex.
Will add
if v1 in self.nodes:
self.nodes.add(v2)
if v2 in self.nodes:
self.nodes.add(v1)
if v1 in nodes and v2 in nodes:
edges.add((v1,v2))
"""
if v1 in self.nodes and self.contains(v2):
self.edges.add((v1,v2))
self.nodes.add(v2)
elif v2 in self.nodes and self.contains(v1):
self.edges.add((v1,v2))
self.nodes.add(v1)
for child in self.children:
child.add_edge(v1,v2)
def rebalance(self):
# rebuild :)
# Or locally reabalnce. Up to depth N.
# turn back to nx.Graph. Rebuild
pass
class DecompForest():
pieces : dict[TreeDecomp]
vertmap : dict[object, TreeDecomp]
def add_vertex(self, v):
if v in self.vertmap:
return self.vertmap[v]
else:
newtree == TreeDecomp.singleton(v)
self.pieces[v] = self.vertmap[v]
return self.vertmap[v]
def add_edge(self, v1,v2):
if v1 in vertmap:
tree1 = vertmap[v1]
elif v2 in vertmap:
pass
def tree_decomp(G):
w, G1 = treewidth.treewidth_min_degree(G)
center_nodes = nx.center(G1)
central_vertex = center_nodes[0]
seen = set()
def dfs(v):
seen.add(v)
children = [dfs(child) for child in G1.neighbors(v) if child not in seen]
return TreeDecomp(nodes=v, edges=set((i,j) for i in v for j in v if (i,j) in G.edges), children=children)
return dfs(central_vertex)
#nx.draw(nx.path_graph(3), with_labels=True)
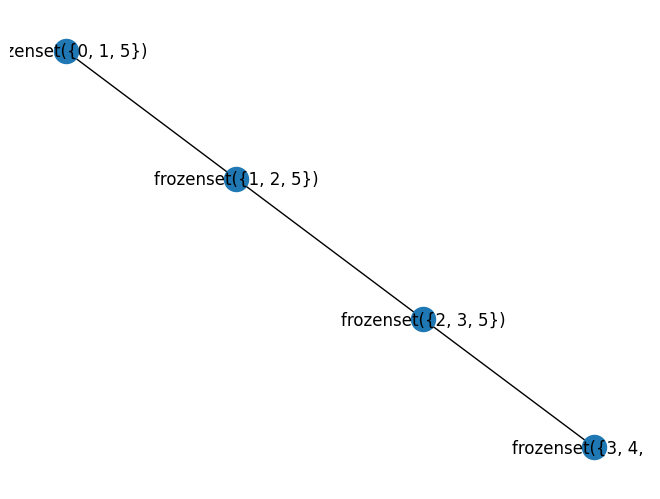
w,G1 = treewidth.treewidth_min_degree(nx.path_graph(5))
print("width", w)
draw_tree(G1)
import pprint
pprint.pprint(tree_decomp(nx.path_graph(5)))
width 1
TreeDecomp(nodes=frozenset({2, 3}),
edges={(2, 3), (3, 2)},
children=[TreeDecomp(nodes=frozenset({1, 2}),
edges={(1, 2), (2, 1)},
children=[TreeDecomp(nodes=frozenset({0, 1}),
edges={(0, 1), (1, 0)},
children=[])]),
TreeDecomp(nodes=frozenset({3, 4}),
edges={(3, 4), (4, 3)},
children=[])])
title: “Treeifying Graphs: A ubiquitous cheat”
Graham mentioned that “programming is fundamentally about trying to define coinductive things (behaviors) inductively (syntax trees).” Something to muse on
Make Tree decomposition. Add hypereclass indirection
Needs interface to request a bundle of edges to be cut.
# graph1 : V -> WeightedSet
def graph1(v): # aparasmeter is starting vertex
yield from [(1, "a"), (2,"b")]
# yeild weighted set, or generator of weighted set
def overlay(g1,g2):
def res(v):
return res
pass
def connect(g1, g2):
def res(v):
pass
return res
def star(g):
pass
https://doisinkidney.com/posts/2024-11-08-formalising-graphs-coinduction.html “There are a few ways to overcome these hurdles: in the functional programming world, huge strides have been made by representing graphs as inductive data types [Erwig 2008; Gibbons 1995] or with typeclasses [Mokhov 2017]. Specifically treating graphs as matrices has also proved useful, especially in elucidating the link between semirings and search algorithms [Backhouse and Carré 1975; Conway 1971; Dolan 2013; Master 2021; Rivas et al. 2015].” Graph V = V -> Neighbors V Hmm niehgbors are weighted sets. sem,iring overlay and connection
Backhouse had a whole book of graph alogorithms right? https://www.academia.edu/39795690/Elements_of_Algorithmic_Graph_Theory_An_Exercise_in_Point_Free_Reasoning
Seem like kidney Wu 2021 is good prior reading https://doisinkidney.com/posts/2021-06-21-icfp-paper.html Algebras for Weighted Search
Graph homomorphisms are also acted on by the permutations of labels. left and right action. so… the slotted tensor thing maybe is like that? It’s a graph homorphism from the symmetry graph of the slots to the labels…
Substitutions vs term homomorphisms
Catlab Csets. ALgerbaic rewriting DPO SPO.
https://doc.sagemath.org/html/en/reference/graphs/sage/graphs/graph_decompositions/rankwidth.html rank width decomposition rw what’s this all about?
https://doc.sagemath.org/html/en/reference/graphs/sage/graphs/graph_decompositions/modular_decomposition.html modular decomposition https://doc.sagemath.org/html/en/reference/graphs/sage/graphs/graph_decompositions/tree_decomposition.html
What is a graph?
What do you want to do on it?
Search a graph spanning tree routing on a graph shortest path maximum flow minimum cut maximum matching minimum spanning tree strongly connected components biconnected components articulation points bridges 2-edge connected components
colorings covers
Tree Decomposition
https://dl.acm.org/doi/10.1145/3689801 Fast and Optimal Extraction for Sparse Equality Graphs https://github.com/mabseher/htd hypertree decomposition https://github.com/PACE-challenge/Treewidth https://pypi.org/project/treedecomp/ https://networkx.org/documentation/latest/reference/algorithms/approximation.html#module-networkx.algorithms.approximation.treewidth
https://en.wikipedia.org/wiki/Decomposition_method_(constraint_satisfaction) https://en.wikipedia.org/wiki/Branch-decomposition
for vs in powerset(vertices):
for p1,p2 in split(vs):
hereedges = [(x,y) if x in p1 and y in y for x,y in edges]
# total splitting of vertices is not necessary though
BoolRef(bag) for bag in powerset(vs)
BoolRef() for bagedges
# union of all aselected bags in all vertices
# one of bags containing egde must be selected
# brute force
graph = [(1,2),(3,4), (4,5)]
# https://docs.python.org/3/library/itertools.html#itertools-recipes
def powerset(iterable):
"powerset([1,2,3]) → () (1,) (2,) (3,) (1,2) (1,3) (2,3) (1,2,3)"
s = list(iterable)
return chain.from_iterable(combinations(s, r) for r in range(len(s)+1))
def all_tree_decomp(V,G):
#vertices = list(set(i for i,j in G) + set(j for i,j in G))
# pick some for this bag
# pick some edges
if len(V) == 0:
return ()
for deledges in powerset(G):
bag = set([i for i,j in deledges] + [j for i,j in deledges])
# one or more children
# all ways of breaking up? multinomial?
# two overlapping subsets?
# Well ok, binary tree decompositions is possibly a different thing, but why not
for bag in powerset(V):
# how do I make progress?
# check if this bag is a separator
is_separator = True
for i,j in G:
if i in bag and j in bag:
is_separator = False
break
if is_separator:
# if it is a separator, then split the graph
#G1 = [(i,j) for i,j in G if i in bag or j in bag]
needed = [(i,j) for i,j in G if i not in bag and j not in bag]
# recursively call the function
for T1 in all_tree_decomp(G1):
for T2 in all_tree_decomp(G2):
yield (bag, T1, T2)
break
def all_tree(active_edge, bag, G):
# each bag will only appear once right?
# eaiser to do bottom up maybe?
for bag in powerset(V):
active = set( i,j for i,j in G if i in bag j not in bag)
dealt_with = set( i,j for i,j in G if i in bag and j in bag)
todo = [(active, dealt_with, bag)]
passive = []
while todo:
active, dealt_with, bag = todo.pop()
for d in passive: # search for other passive sibling bags
passive.append((active, dealt_with, bag))
todo = [(set(range(1,6)), graph)]
while todo:
active, bag = todo.pop()
for newverts in powerset(V - bag) # but has to contain active + 1
for usedactive in powerset(active):
if len(usedactive) == 0:
continue
else:
newbag = usedactive | newverts
todo.append((newverts, newbag, newgraph))
for bag in powerset(V):
def is_tree_decmp(d, G):
# tree decomp
class Node():
bag: set[V]
bagedges : set[E]
children: set[Node]
def treewidth(self):
return max(len(self.bag) - 1, max([c.treewidth() for c in self.children]))
class GraphTree():
here: set[V] # nodes only here
edges: set[E] #egdes between only here and children
children: set[tuple[set[V], GraphTree]]
def color(self, colors):
# take in a list of colors
V = int
Edge = tuple[V,V]
# flat reps
Graph1 = set[Edge]
Graph2 = list[Edge]
Graph3 = dict[V, set[V]]
# structured representations
# kerngihan Lin
def kl(edges):
A = set()
B = set()
Graph canonicalization
group theory
This is neither here nor there kind of. It’s “just” for symmettry breaking during search, which is especially painful in canonization search
caonicalizing graphs via brute force. Come up with a system of serialzing, sort those strings. Not necessarily stable in any sense though graph isomorphism Sims-schreiers
schreir vectors = spanning tree. (?) store group element that would connect to previous node of spanning tree. This is the group union find? Huh.
schreir sims - a canonical form of group element. https://en.wikipedia.org/wiki/Schreier%E2%80%93Sims_algorithm
Stabilizer = subgroup defined as the the group elements that leave a particular elemement unchanged
Schreir generators. If we pick representatives of the cosets of a subgroup, we can generate the subgroup using combined generators and repsdentatives as generators.
Return stabilizer of initial point as collection of schreier generatoras. Orbit stabilizer algorithm
https://en.wikipedia.org/wiki/Group_action
undirected Graph where every neighborhood has the same moves = group action on vertex set. edge pattern is generators. https://en.wikipedia.org/wiki/Cayley_graph Origin is special or no? Stabilizer group of origin are loops. rubiks cube
https://terrytao.wordpress.com/2010/07/10/cayley-graphs-and-the-geometry-of-groups/ subgroups and bundles
a base, special points. What if graph is disconnected?
Consider general graphs as mangled cayley graphs. Even if I was given two cayley graphs is it obvious how to canonicaslize it? The point of gropup theory is to cut down on boring symmettry explosion. Where is this?
cosets partition… partition refinement using group tags?
g = (h, g’) where h is element of subgroup and g’ is caonoical represdentiatvie of coset
from dataclasses import dataclass
@dataclass(frozen=True)
class Perm():
perm : list[int]
@classmethod
def e(self, n):
return Perm(list(range(n)))
def __mul__(self, other):
return Perm([self.perm[p] for p in other.perm])
e3 = Perm.e(3)
assert e3 * e3 == e3
p = Perm([1,0])
assert p * p == Perm.e(2)
assert Perm([1,2,0]) * Perm([2,0,1]) == Perm([0,1,2])
def naive()
Suppose I wanted the automorphism group. Can I generate it?
swaps Generate permutation group. swaps
Also, swaps are kind of an incrementalo strcturue which is good for functional programming maybe.
note that this is a method to generate permutations too. swap to decide which element of remaining in in nth position.
https://en.wikipedia.org/wiki/Steinhaus%E2%80%93Johnson%E2%80%93Trotter_algorithm Steinhaus–Johnson–Trotter algorithm https://en.wikipedia.org/wiki/Heap%27s_algorithm https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle randomly genrate a permutation
def canon(G, N):
swaps = [(i,j) for i in range(N) for j in range(i)]
for
for p in permutations(range(3)):
yield perm_graph(p, G)
If we do a more careful backtracking search, we can prune a lot. We learn partial order constraints as we go. Maybe a difference logic thing would be helpful. We get good strings by ordering the vertices by degree first. We can do a lot of propagation. We can do prefix comparison because we’re being lexicographic.
We could have other representations of graphs. A tree representation follows naturally from Tree Decomposition (kind of. We also need to create a unique tree decomp… or use an ordering that doesn’t care which tree decomp we picked. Hmmmm. best Spanning tree? Again tie breaking here brings in graph canonization. These things need to be considered bolted together). We could then use total tree orderings instead of string orderings.
“Natrual graph orderings” like that minor homomorphism thing. https://en.wikipedia.org/wiki/Robertson%E2%80%93Seymour_theorem
Maybe this is more sensical for tree with backref ids. Which numbers do we put in the backref ids to make canonical. Then the tree structure exists a priori.
# to get cycles. Orbits under subgroup consisting of p^n. Generated by <p>
def cycles(p):
found = set()
for i in range(len(p)):
if i not in found:
cycle = []
j = i
while j not in cycle:
cycle.append(j)
j = p[j]
yield cycle
found.update(cycle)
list(cycles([1,0,2]))
def inv(p):
inv = [0]*len(p)
for i in range(len(p)):
inv[p[i]] = i
return inv
def orbit(ps, n):
found = set()
done = False
while not done:
done = False
for f in found:
for p in ps:
e = p[f]
if e not in found:
done = False
found.add(e)
Perm = list[int]
# orbit of is fixed point of this operation starting from {x}.
def step(G : list[Perm], s : set[int]) -> set[int]: # G is list/set of permutations
return s | {p[i] for p in G for i in s}
def is_inv(G,s):
return s == step(G,s)
# can apply standard seminaive trick
# can retain "proof" / path as group union find.
# schreier vectors
# base
# strong generating set
[[0, 1], [2]]
def termact(p, t):
head,*args = t
return (head,*[termact(p,a) for a in args])
def canon(t, N):
# a silly implementation.
min([ termact(p,t) for p in itertools.permutations(range(N))])
import metis
import networkx as nx
G = nx.path_graph(7)
edgecuts, parts = metis.part_graph(G,3)
print(edgecuts, parts)
print(nx.community.kernighan_lin_bisection(G)) # anneal a cut by node swapping
print(list(nx.community.girvan_newman(G))) # remove edges from graph
import sqlite3
import networkx as nx
def db_of_graph(conn, G):
con.executemany("INSERT INTO nodes VALUES (?)", map(lambda v : (v,), G.nodes))
con.executemany("INSERT INTO edges VALUES (?, ?)", G.edges)
if not G.is_directed():
con.executemany("INSERT INTO edges VALUES (?, ?)", [(j,i) for i,j in G.edges])
def graph_of_db(con):
G = nx.DiGraph()
res = con.execute("SELECT * FROM nodes")
G.add_nodes_from(map(lambda x: x[0], res.fetchall()))
res = con.execute("SELECT * FROM edges")
G.add_edges_from(res.fetchall())
return G
def query_of_graph(G,unique=False):
"""Unique will give subgraph isomorphism"""
selects = []
froms = []
wheres = []
for node in G:
froms += [f"nodes AS v{node}"]
selects += [f"v{node}.v AS v{node}"]
for i, (a,b) in enumerate(G.edges):
froms += [f"edges as e{i}"]
wheres += [f"e{i}.src = v{a}.v" , f"e{i}.dst = v{b}.v"]
if unique:
for node in G:
for node2 in G:
if node != node2:
wheres += [f"v{node} != v{node2}"]
sql = "SELECT " + ", ".join(selects) + \
"\nFROM " + ", ".join(froms) + \
"\nWHERE " + " AND ".join(wheres)
return sql
def clear_db(con):
con.execute("DELETE FROM nodes")
con.execute("DELETE FROM edges")
G = nx.path_graph(7, create_using=nx.DiGraph)
lhs = nx.path_graph(3, create_using=nx.DiGraph)
con = sqlite3.connect(":memory:")
con.execute("CREATE TABLE nodes(v)")
con.execute("CREATE TABLE edges(src,dst)")
db_of_graph(con, G)
res = con.execute(query_of_graph(lhs))
print(res.fetchall())
# Result: [(0, 1, 2), (1, 2, 3), (2, 3, 4), (3, 4, 5), (4, 5, 6)]
[(0, 1, 2), (1, 2, 3), (2, 3, 4), (3, 4, 5), (4, 5, 6)]
res = con.execute(query_of_graph(G))
print(query_of_graph(G))
res.fetchall()
SELECT v0.v AS v0, v1.v AS v1, v2.v AS v2, v3.v AS v3, v4.v AS v4, v5.v AS v5, v6.v AS v6
FROM nodes AS v0, nodes AS v1, nodes AS v2, nodes AS v3, nodes AS v4, nodes AS v5, nodes AS v6, edges as e0, edges as e1, edges as e2, edges as e3, edges as e4, edges as e5
WHERE e0.src = v0.v AND e0.dst = v1.v AND e1.src = v1.v AND e1.dst = v2.v AND e2.src = v2.v AND e2.dst = v3.v AND e3.src = v3.v AND e3.dst = v4.v AND e4.src = v4.v AND e4.dst = v5.v AND e5.src = v5.v AND e5.dst = v6.v
[(0, 1, 2, 3, 4, 5, 6)]
nx.draw(G, with_labels=True)
clear_db(con)
G = nx.path_graph(4)
db_of_graph(con, G)
res = con.execute(query_of_graph(G))
res.fetchall()
# undirected graph
[(1, 0, 1, 0),
(1, 0, 1, 2),
(0, 1, 0, 1),
(0, 1, 2, 1),
(0, 1, 2, 3),
(2, 1, 0, 1),
(2, 1, 2, 1),
(2, 1, 2, 3),
(1, 2, 1, 0),
(1, 2, 1, 2),
(1, 2, 3, 2),
(3, 2, 1, 0),
(3, 2, 1, 2),
(3, 2, 3, 2),
(2, 3, 2, 1),
(2, 3, 2, 3)]
The two isomorphisms of the path graph
res = con.execute(query_of_graph(G,unique=True))
res.fetchall()
[(0, 1, 2, 3), (3, 2, 1, 0)]
Here we find a mapping into a color table considered as a complete graph The lack of self edges in the color graph means no
print(graph_of_db(con))
"DELETE FROM nodes WHERE nodes.v = ?"
"DELETE FROM edges where edges.src = ? OR edges.dst = ?"
clear_db(con)
colors = nx.complete_graph(2) # a two coloring
db_of_graph(con,colors)
# symmetrize. Maybe db_of_graph should do this. if not isinstanc(G,nx.DiGraph)
#con.execute("INSERT INTO edges SELECT edges.dst, edges.src FROM edges")
res = con.execute("SELECT * FROM edges")
res = print(res.fetchall())
res = con.execute(query_of_graph(G)) # two dimer colorings
print(res.fetchall())
# [(1, 0, 1, 0, 1, 0, 1), (0, 1, 0, 1, 0, 1, 0)]
DiGraph with 4 nodes and 6 edges
[(0, 1), (1, 0)]
[(1, 0, 1, 0), (0, 1, 0, 1)]